题目内容
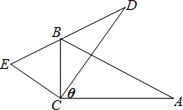
【题目】如图,△ABC中,∠ACB=90°,∠A=25°,若以点C为旋转中心,将△ABC旋转θ度到△DEC的位置,使点B恰好落在边DE上,则θ等于_____.
【答案】50°
【解析】
先根据互余计算出∠ABC=65°,再根据旋转的性质得CB=CE,∠BCE=∠ACD=θ,∠E=∠ABC=65°,则根据等腰三角形的性质得∠E=∠CBE=65°,然后在△BCE中根据三角形内角和定理可计算出∠BCE的度数.
解:∵∠ACB=90°,∠A=25°,
∴∠ABC=65°,
∵△ABC旋转θ°到△DEC的位置,使点B恰好落在边DE 上,
∴CB=CE,∠BCE=∠ACD=θ,∠E=∠ABC=65°,
∴∠E=∠CBE=65°,
∴∠BCE=180°-2×65°=50°,
即θ=50°.
故答案为:50°

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目