题目内容
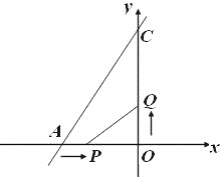
【题目】如图，已知，在直角坐标系xOy中，直线 y=
x+8与x轴、y轴分别交于点A、C，点P从A点开始以1个单位/秒的速度沿x轴向右移动，点Q从O点开始以2个单位/秒的速度沿y轴向上移动，如果P、Q两点同时出发，经过几秒钟，能使△PQO的面积为8个平方单位．com
【答案】经过2秒，4秒或 3+
秒能使△PQO的面积为8个平方单位.
【解析】
分点P在线段OA上和点P与点O重合或在线段OA的延长线上两种情况讨论即可.
直线AC与x轴交于点A（－6，0），与y轴交于点C（0，8），
∴OA=6，OC=8．
设经过x秒钟，能使△PQO的面积为8个平方单位，
则Rt△PQO的高OQ为2x，
当0<x<6 时，点P在线段OA上，底OP为6－x，
可列方程
=8，
解得：x1=2，x2=4 ；
当 x≥6时，点P与点O重合或在线段OA的延长线上，底OP为x－6，
可列方程
，
解得：x1=3+，x2=3-，而x2=3-不合题意舍去；
综上所述，经过2秒，4秒或 x2=3+秒能使△PQO的面积为8个平方单位.
练习册系列答案
相关题目
