题目内容
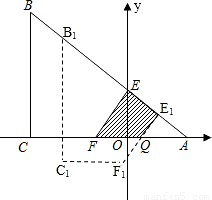
如图,等腰直角三角形纸片ABC中,AC=BC=4,∠ACB=90°,直角边AC在x轴上,B点在第二象限,A(1,0),AB交y轴于E,将纸片过E点折叠使BE与EA所在直线重合,得到折痕EF(F在x轴上),再展开还原沿EF剪开得到四边形BCFE,然后把四边形BCFE从E点开始沿射线EA平移,至B点到达A点停止.设平移时间为t(s),移动速度为每秒1个单位长度,平移中四边形BCFE与△AEF重叠的面积为S.(1)求折痕EF的长;
(2)是否存在某一时刻t使平移中直角顶点C经过抛物线y=x2+4x+3的顶点?若存在,求出t值;若不存在,请说明理由;
(3)直接写出S与t的函数关系式及自变量t的取值范围.
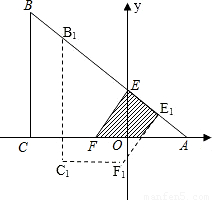
【答案】分析:(1)因为折叠后BE与EA所在直线重合推出EF=EA,OA=OE=1,可求出AE,EF的值.
(2)设CP∥BA交Y轴于P,推出△POC为等腰直角三角形,求出点C移动的水平距离后可求出时间.
(3)本题考查的是分段函数的知识.
解答: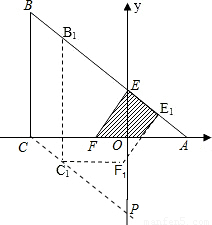 解:(1)∵折叠后BE与EA所在直线重合
解:(1)∵折叠后BE与EA所在直线重合
∴FE⊥EA又Rt△ABC中AC=BC
∴∠CAB=45°
∴EF=EA
∵A(1,0)
∴OA=OE=1,AE=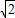
∴折痕EF=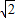 .
.
(2)存在,设CP∥BA交Y轴于P,
则△POC为等腰直角三角形,直角顶点C在射线CP上移动
∵AC=4,OA=1
∴OC=OP=3
∴C(-3,0),P(0,-3)可求得PC所在直线解析式为:y=-x-3
∵直角顶点C从(-3,0)位置移动到(-2,-1)时,水平移动距离为|-2-(-3)|=1(长度单位)
∴直角顶点C从开始到经过此抛物线顶点移动的时间t=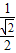 =
=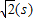 .
.
(3)当0≤t≤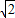 时,
时,
四边形BCFE与△AEF重叠的面积为:直角梯形EFQE 1,
故面积为:S= (EF+E1Q)×EE1=
(EF+E1Q)×EE1= t(
t(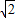 -t+
-t+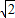 )=-
)=- t2+
t2+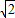 t,
t,
同理可得出其它函数解析式:
s=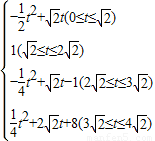 .
.
点评:本题综合考查的是分段函数的知识,二次函数的综合运用以及三角函数的应用.难度较大.
(2)设CP∥BA交Y轴于P,推出△POC为等腰直角三角形,求出点C移动的水平距离后可求出时间.
(3)本题考查的是分段函数的知识.
解答:
 解:(1)∵折叠后BE与EA所在直线重合
解:(1)∵折叠后BE与EA所在直线重合∴FE⊥EA又Rt△ABC中AC=BC
∴∠CAB=45°
∴EF=EA
∵A(1,0)
∴OA=OE=1,AE=
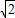
∴折痕EF=
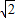 .
.(2)存在,设CP∥BA交Y轴于P,
则△POC为等腰直角三角形,直角顶点C在射线CP上移动
∵AC=4,OA=1
∴OC=OP=3
∴C(-3,0),P(0,-3)可求得PC所在直线解析式为:y=-x-3
∵直角顶点C从(-3,0)位置移动到(-2,-1)时,水平移动距离为|-2-(-3)|=1(长度单位)
∴直角顶点C从开始到经过此抛物线顶点移动的时间t=
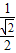 =
=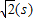 .
.
(3)当0≤t≤
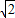 时,
时,四边形BCFE与△AEF重叠的面积为:直角梯形EFQE 1,
故面积为:S=
 (EF+E1Q)×EE1=
(EF+E1Q)×EE1= t(
t(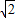 -t+
-t+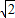 )=-
)=- t2+
t2+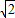 t,
t,同理可得出其它函数解析式:
s=
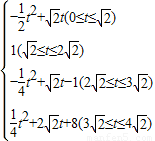 .
.点评:本题综合考查的是分段函数的知识,二次函数的综合运用以及三角函数的应用.难度较大.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
 如图,等腰直角三角形ABC绕C点按顺时针旋转到△A1B1C1的位置(A、C、B1在同一直线上),∠B=90°,如果AB=1,那么AC运动到A1C1所经过的图形的面积是
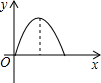
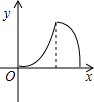
如图,等腰直角三角形ABC绕C点按顺时针旋转到△A1B1C1的位置(A、C、B1在同一直线上),∠B=90°,如果AB=1,那么AC运动到A1C1所经过的图形的面积是 如图,等腰直角三角形ABC的腰长与正方形DEFG的边长相符,且边AC与DE在同一直线l上,△ABC从如图所示的起始位置(A、E重合),沿直线l水平向右平移,直至C、D重合为止.设△ABC与正方形DEFG重叠部分的面积为y,平移的距离为x,则y与x之间的函数关系大致是( )
如图,等腰直角三角形ABC的腰长与正方形DEFG的边长相符,且边AC与DE在同一直线l上,△ABC从如图所示的起始位置(A、E重合),沿直线l水平向右平移,直至C、D重合为止.设△ABC与正方形DEFG重叠部分的面积为y,平移的距离为x,则y与x之间的函数关系大致是( )

 如图,等腰直角三角形ABC中,∠BAC=90°,D、E分别为AB、AC边上的点,AD=AE,AF⊥BE交BC于点F,过点F作FG⊥CD交BE的延长线于点G,交AC于点M.
如图,等腰直角三角形ABC中,∠BAC=90°,D、E分别为AB、AC边上的点,AD=AE,AF⊥BE交BC于点F,过点F作FG⊥CD交BE的延长线于点G,交AC于点M. 如图,等腰直角三角形△ABC中,∠ACB=90°,点D是BC的中点,CE⊥AD于点F交AB于点E,CH是AB上的高交AD于点G.
如图,等腰直角三角形△ABC中,∠ACB=90°,点D是BC的中点,CE⊥AD于点F交AB于点E,CH是AB上的高交AD于点G. 如图,等腰直角三角形AEF的顶点E在等腰直角三角形ABC的边BC上.AB的延长线交EF于D点,其中∠AEF=∠ABC=90°.
如图,等腰直角三角形AEF的顶点E在等腰直角三角形ABC的边BC上.AB的延长线交EF于D点,其中∠AEF=∠ABC=90°.