题目内容
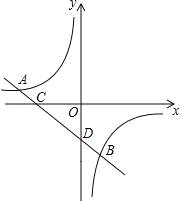
【题目】如图,直线y=k1x+b1与反比例函数y=![]() 的图象及坐标轴依次相交于A、B、C、D四点,且点A坐标为(﹣3,
的图象及坐标轴依次相交于A、B、C、D四点,且点A坐标为(﹣3,![]() ),点B坐标为(1,n).
),点B坐标为(1,n).
(1)求反比例函数及一次函数的解析式;
(2)求证:AC=BD;
(3)若将一次函数的图象上下平移若干个单位后得到y=k1x+n,其与反比例函数图象及两坐标轴的交点仍然依次为A、B、C、D.(2)中的结论还成立吗?请写出理由,对于任意k<0的直线y=kx+b.(2)中的结论还成立吗?(请直接写出结论)

【答案】(1)y=﹣![]() x﹣1(2)证明见解析(3)①成立②成立
x﹣1(2)证明见解析(3)①成立②成立
【解析】
试题分析:(1)用待定系数法求出直线解析式和反比例函数解析式;
(2)确定出点A,B,C,D,坐标,利用两点间距离公式求解得AC=BD;
(3)①确定出点A,B,C,D,坐标,利用两点间距离公式求解得AC=BD;
②确定出点A,B,C,D,坐标,利用两点间距离公式求解得AC=BD;
试题解析:(1)∵点A坐标为(﹣3,![]() ),且在反比例函数y=
),且在反比例函数y=![]() 的图象上,
的图象上,
∴k2=xy=﹣3×![]() =﹣
=﹣![]() ,
,
∴反比例函数的解析式为:y=﹣![]() ;
;
∵点B坐标为(1,n),且在反比例函数y=![]() 的图象上,
的图象上,
∴n=﹣![]() ,
,
∴点B坐标为(1,﹣![]() );
);
∴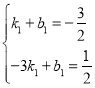 ,
,
解得: ,
,
∴一次函数的解析式为:y=﹣![]() x﹣1;
x﹣1;
(2)∵当x=0时,y=﹣1,则点D的坐标为:(0,﹣1);
当y=0时,x=﹣2,则点C的坐标为:(﹣2,0);
∴AC=![]() =
=![]() ,BD=
,BD= =
=![]() ,
,
∴AC=BD;
(3)①成立,
理由:∵将一次函数的图象上下平移若干个单位后得到y=k1x+n,
∴y=﹣![]() x+n,
x+n,
∴C(2n,0),D(0,n),
∵反比例函数的解析式为:y=﹣![]() 和一次函数y=﹣
和一次函数y=﹣![]() x+n,
x+n,
∴它两的交点坐标为A(n+![]() ,
,![]() ),B(n﹣
),B(n﹣![]() ,
,![]() ),
),
∴AC=![]() ,
,
BD=![]() ,
,
∴AC=BD
②AC=BD,
理由:同①的方法求出直线y=kx+b与x,y轴的交点坐标C(﹣![]() ,0),D(0,b),
,0),D(0,b),
联立直线解析式和反比例函数解析式y=﹣![]() 求出交点坐标A(
求出交点坐标A(![]() ,b+
,b+![]() ),B(
),B(![]() ,b+
,b+![]() ),
),
用平面坐标系内,两点间的距离公式求解得,AC=BD.

 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案【题目】某校举行“社会主义核心价值观”演讲比赛,学校对30名参赛选手的成绩进行了分组统计,结果如下表:
分数x(分) | 4≤x<5 | 5≤x<6 | 6≤x<7 | 7≤x<8 | 8≤x<9 | 9≤x<10 |
频数 | 2 | 6 | 8 | 5 | 5 | 4 |
由上可知,参赛选手分数的中位数所在的分数段为( )
A. 5≤x<6B. 6≤x<7C. 7≤x<8D. 8≤x<9
【题目】本学期实验中学组织开展课外兴趣活动,各活动小班根据实际情况确定了计划组班人数,并发动学生自愿报名,报名人数与计划人数的前5位情况如下.若用同一小班的报名人数与计划人数的比值大小来衡量进入该班的难易程度,则由表中数据,可预测( )
小班名称 | 奥数 | 写作 | 舞蹈 | 篮球 | 航模 |
报名人数 | 215 | 201 | 154 | 76 | 65 |
小班名称 | 奥数 | 舞蹈 | 写作 | 合唱 | 书法 |
计划人数 | 120 | 100 | 90 | 80 | 70 |
A.奥数比书法容易
B.合唱比篮球容易
C.写作比舞蹈容易
D.航模比书法容易

