Question

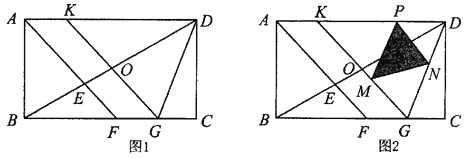
【题目】如图，在△ABC中，AB=AC=5，AB边上的高CD=4.点P从点A出发，沿AB以每秒3个单位长度的速度向终点B运动.当点P不与点A、B重合时，过点P作PQ⊥AB，交边AC或边BC于点Q，以PQ为边向右侧作正方形PQMN.设正方形PQMN与△ABC重叠部分图形的面积为S（平方单位），点P运动的时间为t（秒）.

（1）求tanB的值.

（2）求点M落在边BC上时t的值.

（3）当正方形PQMN与△ABC重叠部分为四边形时，求S与t之间的函数关系式.

（4）边BC将正方形PQMN的面积分为两部分时，设这两部分的面积比为k.当时，直接写出t的取值范围.

Answer 1

【答案】（1）；（2）当点M落在BC边上时，t=.

（3）；

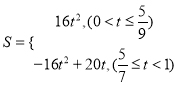（4）＜t≤，1≤t＜

【解析】试题分析：（1）根据勾股定理求出AD的长，然后可求的BD，代入锐角三角函数即可求解；

（2）当点M落在BC边上时， PQ=PN=MN=4t, BN=2t，然后列方程求解即可；

（3）分两种情况：当0＜t≤时，当≤t＜1时，分别求面积即可；

（4）根据上面所求直接判断即可.

试题解析：（1）∵CD⊥AB，

∴∠ADC=∠ADB= 90°.

∵在Rt△ACD中， ，

∴BD=AB－AD=5－3=2．

∴在Rt△BCD中， .

（2）当点M落在BC边上时， PQ=PN=MN=4t, BN=2t.

∴3t+4t+2t=5,

∴t=.

（3）当0＜t≤时，S=16t．

当≤t＜1时， ．

（4）＜t≤，1≤t＜．