题目内容
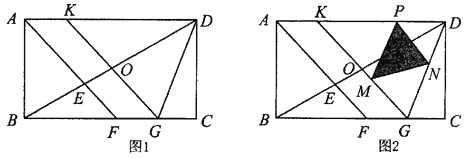
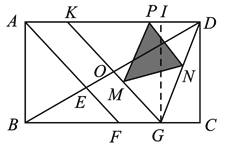
【题目】如图l,在矩形ABCD中,BC>AB,∠BAD的平分线AF与BD、BC分别交于点E、F,点O是BD的中点,直线OK∥AF,交AD于点K,交BC于点G.
(1)求证:△DOK≌△BOG;
(2)求证:AB+AK=BG:
(3)如图2,若KD=KG=2,点P是线段KD上的动点(不与点D、K重台),PM∥DG交KG于点M,PN∥KG交DG于点N,设PD=x,S△PMN=y,求出y与x的函数关系式.
【答案】(1)证明见解析(2)![]()
【解析】(1)先根据AAS判定△DOK≌△BOG,(2)再根据等腰三角形ABF和平行四边形AFKG的性质,得出结论BG=AB+AK;(3)利用△DKG∽△PKM∽△DPN,由相似三角形的性质求出y与x的函数关系式.
解:(1)∵在矩形ABCD中,AD∥BC
∴∠KDO=∠GBO,∠DKO=∠BGO
∵点O是BD的中点
∴DO=BO
∴△DOK≌△BOG(AAS)
(2)∵四边形ABCD是矩形
∴∠BAD=∠ABC=90°,AD∥BC
又∵AF平分∠BAD
∴∠BAF=∠BFA=45°
∴AB=BF
∵OK∥AF,AK∥FG
∴四边形AFGK是平行四边形
∴AK=FG
∵BG=BF+FG
∴BG=AB+AK
(3)解法一:
如图,过点G作GI⊥KD于点I,
由(2)知,四边形AFGK是平行四边形,△ABF为等腰直角三角形.
∴AF=KG=2, ![]() .
.
∵四边形ABCD是矩形,
∴GI=AB=![]() ,
,![]() 。
。
∵PD=x
∴PK=2﹣x
∵PM∥DG,PN∥KG
∴四边形PMGN是平行四边形,△DKG∽△PKM∽△DPN
∴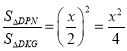 ,
,
即![]()
同理, ![]()
![]()
![]()
![]() .
.
解法二:
如图,过点P作PQ⊥KG于点Q,
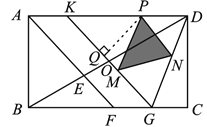
∴KD=KG,∠KDG=∠KGD
又∵PN∥KG
∴∠PND=∠KGD
∴∠PND=∠KDFG
∴PN=PD=x.
∵AF∥KG,
∴∠PKM=∠DAF=45°,又∵PK=2﹣x
∴![]()
又∵PN∥KG,
![]() .
.
“点睛”本题主要考查了矩形的性质以及平行四边形的性质,解题时需要运用全等三角形的判定与性质.解答此题的关键是运用相似三角形的面积之比等于相似比的平方这一性质,并根据图形面积的等量关系列出方程进行求解,难度较大,具有一定的综合性.

 阅读快车系列答案
阅读快车系列答案