题目内容
【题目】将等腰直角△ABC斜放在平面直角坐标系中,使直角顶点C与点(1,0)重合,点A的坐标为(﹣2,1).
(1)求△ABC的面积S;
(2)求直线AB与y轴的交点坐标.
【答案】解:(1)过点A作AD⊥x轴,垂足为D.
∵C(1,0),A(﹣2,1),
∴AD=1,DC=1﹣(﹣2)=3,
∴AC2=AD2+DC2=10,
∴S△ABC=![]() AC2=5;
AC2=5;
(2)过点B作BE⊥x轴,垂足为E,
∴∠ADC=∠CEB=90°,
∴∠CAD+∠ACD=90°,
∵∠ACB=90°,
∴∠BCE+∠ACD=90°,
∴∠CAD=∠BCE.
在△ADC和△CEB中,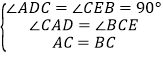 ,
,
∴△ADC≌△CEB,
∴CD=BE=3,CE=AD=1,
∴OE=2,
∴点B的坐标为(2,3).
设直线AB的解析式为y=kx+b,则![]() ,
,
解得![]() ,
,
∴y=![]() x+2.
x+2.
当x=0时,y=2,
∴直线AB交y轴于点(0,2).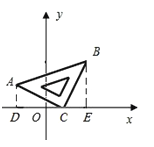
【解析】(1)过点A作AD⊥x轴,垂足为D,根据A、C两点的坐标可求出AD和DC,根据勾股定理可求出AC2 , 即可求出等腰直角△ABC的面积;
(2)要求直线AB与y轴的交点坐标,只需求出直线AB的解析式,只需求出点B的坐标,过点B作BE⊥x轴,垂足为E,易证△ADC≌△CEB,即可得到BE和CE,
从而得到点B的坐标,问题得以解决.

练习册系列答案
相关题目