题目内容
【题目】如图,已知AB为半圆O的直径,C为半圆O上一点,连接AC,BC,过点O作OD⊥AC于点D,过点A作半圆O的切线交OD的延长线于点E,连接BD并延长交AE于点F.
(1)求证:AEBC=ADAB;
(2)若半圆O的直径为10,sin∠BAC= ![]() ,求AF的长.
,求AF的长.
【答案】
(1)
证明:∵AB为半圆O的直径,
∴∠C=90°,
∵OD⊥AC,
∴∠CAB+∠AOE=90°,∠ADE=∠C=90°,
∵AE是切线,
∴OA⊥AE,
∴∠E+∠AOE=90°,
∴∠E=∠CAB,
∴△EAD∽△ABC,
∴AE:AB=AD:BC,
∴AEBC=ADAB.
(2)
解:
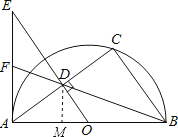
作DM⊥AB于M,
∵半圆O的直径为10,sin∠BAC= ![]() ,
,
∴BC=ABsin∠BAC=6,
∴AC= ![]() =8,
=8,
∵OE⊥AC,
∴AD= ![]() AC=4,OD=
AC=4,OD= ![]() BC=3,
BC=3,
∵sin∠MAD= ![]() =
= ![]() ,
,
∴DM= ![]() ,AM=
,AM= ![]() =
= ![]() =
= ![]() ,BM=AB﹣AM=
,BM=AB﹣AM= ![]() ,
,
∵DM∥AE,
∴ ![]() ,
,
∴AF= ![]() .
.
【解析】(1)只要证明△EAD∽△ABC即可解决问题.(2)作DM⊥AB于M,利用DM∥AE,得 ![]() 求出DM、BM即可解决问题.本题考查切线的性质、勾股定理、三角函数、平行线分线段成比例定理、相似三角形的判定和性质等知识,解题的关键是正确寻找相似三角形,学会添加常用辅助线,属于中考常考题型.
求出DM、BM即可解决问题.本题考查切线的性质、勾股定理、三角函数、平行线分线段成比例定理、相似三角形的判定和性质等知识,解题的关键是正确寻找相似三角形,学会添加常用辅助线,属于中考常考题型.

练习册系列答案
相关题目





