题目内容
【题目】如图,已知![]() ,
,![]() ,
,![]() ,点
,点![]() 是射线
是射线![]() 上的一个动点(点
上的一个动点(点![]() 与点
与点![]() 不重合),点
不重合),点![]() 是线段
是线段![]() 上的一个动点(点
上的一个动点(点![]() 与点
与点![]() 不重合),连接
不重合),连接![]() ,过点
,过点![]() 作
作![]() 的垂线,交射线
的垂线,交射线![]() 于点
于点![]() 连接
连接![]() .设
.设![]()
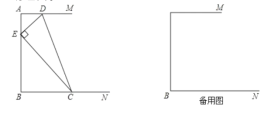
(1)当![]() 时,求
时,求![]() 关于
关于![]() 的函数关系式,并写出它的定义域;
的函数关系式,并写出它的定义域;
(2)在(1)的条件下,取线段![]() 的中点
的中点![]() ,连接
,连接![]() ,若
,若![]() ,求
,求![]() 的长;
的长;
(3)如果动点![]() 在运动时,始终满足条件
在运动时,始终满足条件![]() 那么请探究:
那么请探究:![]() 的周长是否随着动点
的周长是否随着动点![]() 的运动而发生变化?请说明理由。
的运动而发生变化?请说明理由。
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 的周长不变,理由见解析
的周长不变,理由见解析
【解析】
(1)由△AED∽△BCE,得出其对应边成比例,进而可得出x与y的关系式;
(2)可过D点作DH⊥BN于H,求出BC的值,即y的值,进而可求解x的值;
(3)△BCE的周长为一定值,由于题中满足条件AD+DE=AB,且△AED∽△BCE,由于相似三角形的周长比即为其对应边的比,所以可得其周长不变.
(1)由题中条件可得△AED∽△BCE,
∴![]() ,
,
∵AE=x,BC=y,AB=4,AD=1
∴BE=4x,
∴![]() ,
,
∴![]() ;
;
(2)∵DE⊥EC,
∴∠DEC=90°,
又∵DF=FC,
∴DC=2EF=2×2.5=5,
如图所示,过D点作DH⊥BN于H,则DH=AB=4,
∴Rt△DHC中, ![]() ,
,
∴BC=BH+HC=1+3=4,即y=4,
∴![]()
解得:![]() ,
,
∴AE=2;

(3)△BCE的周长不变. 理由如下:
![]() ,BE=4x,
,BE=4x,
设AD=m,则DE=4m,
∵∠A=90,
∴DE2=AE2+AD2即,(4m)2=x2+m2
∴![]() ,
,
由(1)知:△AED∽△BCE,
∴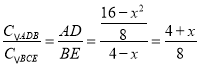
∴![]()
∴△BCE的周长不变.

【题目】已知抛物线C:y=x2+2x﹣3.
抛物线 | 顶点坐标 | 与x轴交点坐标 | 与y轴交点坐标 | |
抛物线C:y=x2+2x﹣3 | A(_____) | B(_____) | (1,0) | (0,﹣3) |
变换后的抛物线C1 | ______ | ______ | ______ | ______ |
(1)补全表中A,B两点的坐标,并在所给的平面直角坐标系中画出抛物线C.
(2)将抛物线C上每一点的横坐标变为原来的2倍,纵坐标变为原来的![]() ,可证明得到的曲线仍是抛物线,(记为C1),求抛物线C1对应的函数表达式.
,可证明得到的曲线仍是抛物线,(记为C1),求抛物线C1对应的函数表达式.