题目内容
【题目】已知抛物线![]() .
.
(1)该抛物线的对称轴是![]() ________.
________.
(2)该抛物线与![]() 轴交于点
轴交于点![]() ,点
,点![]() 与
与![]() 轴交于点
轴交于点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,若此抛物线的对称轴上的点
,若此抛物线的对称轴上的点![]() 满足
满足![]() ,则点
,则点![]() 的纵坐标
的纵坐标![]() 的取值范围是________.
的取值范围是________.
【答案】2 ![]() 或
或![]()
【解析】
(1)根据抛物线的对称轴为![]() 进行求解;
进行求解;
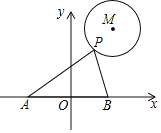
(2)根据二次函数的性质可求出点B,C的坐标,作BC的垂线交对称轴于点F,以点F为圆心,以FB为半径作⊙F,得到△ABC的外接圆,根据两点间距离公式可求出圆心F的坐标以及外接圆半径,然后根据圆的性质可得点P在第一象限时,点![]() 的纵坐标
的纵坐标![]() 的取值范围,同理可得点P在第四象限时,点
的取值范围,同理可得点P在第四象限时,点![]() 的纵坐标
的纵坐标![]() 的取值范围.
的取值范围.
解:(1)该抛物线的对称轴是![]() ,
,
故答案为:2;
(2)∵点![]() 的坐标为
的坐标为![]() ,抛物线的对称轴是
,抛物线的对称轴是![]() ,
,
∴点B的坐标为(3,0),
将点![]() 代入
代入![]() 可得:a=1,
可得:a=1,
∴4a-1=3,即点C的坐标为(0,3),
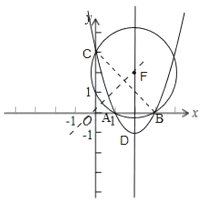
如图,作BC的垂线交对称轴于点F,以点F为圆心,以FB为半径作⊙F,得到△ABC的外接圆,设点F坐标为(2,m),
由FA=FC可得:![]() ,
,
解得:m=2,
∴点F的坐标为(2,2),FA=![]() ,
,
∴当∠APB<∠ACB,且点P在第一象限时,点![]() 的纵坐标
的纵坐标![]() 的取值范围是:
的取值范围是:![]() ,
,
同理可得,点P在第四象限时,点![]() 的纵坐标
的纵坐标![]() 的取值范围是
的取值范围是![]() .
.
综上所述,点的纵坐标![]() 的取值范围是:
的取值范围是:![]() 或
或![]() ,
,
故答案为:![]() 或
或![]() .
.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目