题目内容
【题目】如图，在四边形ABCD中，∠B=∠D=90°，AE平分∠BAD交CD于点E，过点C作CF∥AE交AB于点F． 求证：CF平分∠BCD．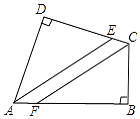
【答案】解：∵∠B=∠D=90°， ∴∠DAB+∠BCD=180°，
∵EA∥CF，
∴∠3=∠1，
∵∠3+∠4=90°，
∴∠1+∠4=90°，
∴∠2+∠5=90°，
∵AE平分∠BAD交CD于点E，
∴∠4=∠6，
∴∠4=∠5，
∴∠1=∠2，
∴CF平分∠BCD．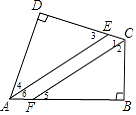
【解析】根据四边形的内角和得到∠DAB+∠BCD=180°，根据平行线的性质得到∠3=∠1，等量代换得到∠2+∠5=90°，根据角平分线的定义得到∠4=∠6，等量代换得到∠1=∠2，于是得到结论．
【考点精析】关于本题考查的平行线的性质和多边形内角与外角，需要了解两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补；多边形的内角和定理：n边形的内角和等于（n-2）180°.多边形的外角和定理：任意多边形的外角和等于360°才能得出正确答案．
【题目】如果10b=n，那么b为n的劳格数，记为b=d（n），由定义可知：10b=n与b=d（n）所表示的b、n两个量之间的同一关系．例如：101=10，d（10）=1
（1）根据劳格数的定义，填空：d（102）= ，
（2）劳格数有如下运算性质：若m、n为正数，则d（mn）=d（m）+d（n），d（ 
）=d（m）﹣d（n）． 根据运算性质，填空： 
=（a为正数），若d（2）=0.3010，则d（16）= ， d（5）= ，
（3）如表中与数x对应的劳格数d（x）有且只有两个是错误的
x | 1.5 | 3 | 5 | 6 | 8 | 9 | 18 | 27 |
d（x） | 3a﹣b+c | 2a+b | a﹣c | 1+a+b+c | 3﹣3a+3c | 4a+2b | 3﹣b﹣2c | 6a+3b |
请找出错误的劳格数，并表格中直接改正．
