题目内容
【题目】![]() 和
和![]() 都是等腰直角三角形,其中
都是等腰直角三角形,其中![]() ,
,![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 的度数.
的度数.

【答案】(1)证明见解析;(2)∠EBD=140°.
【解析】
(1)根据同角的余角相等可得∠BCD=∠ACE,利用SAS可证明△BCD≌△ACE,根据全等三角形的性质即可得结论;(2)延长DB,交AE与F,交EC于G,由(1)得△BCD≌△ACE,可得∠AEC=∠BDC,根据对顶角相等可得∠EFD=∠ECD=90°,利用外角性质求出∠EBD的度数即可.
(1)∵![]() ,
,
∴∠BCD+∠BCE=∠ACE+∠BCE,
∴∠BCD=∠ACE,
在△BCD和△ACE中,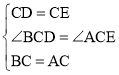 ,
,
∴△BCD≌△ACE,
∴BD=AE.
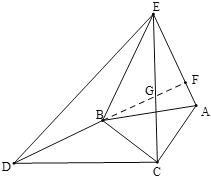
(2)延长DB,交AE与F,交EC于G,
∵△BCD≌△ACE,
∴∠BDC=∠AEC,
∵∠DGC=∠EGF,∠ECD=90°,
∴∠EFD=∠ECD=90°,
∵∠AEB=50°,
∴∠EBD=∠EFD+∠AEB=90°+50°=140°.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目