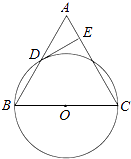
题目内容
【题目】在△ABC中,∠A=90°,点D在线段BC上,∠EDB= ![]() ∠C,BE⊥DE,垂足E,DE与AB相交于点F.
∠C,BE⊥DE,垂足E,DE与AB相交于点F.
(1)当AB=AC时,(如图1),
① ∠EBF=°;
②求证:BE= 1 2 FD;
(2)当AB=kAC时(如图2),求 ![]() 的值(用含k的式子表示).
的值(用含k的式子表示).
【答案】
(1)22.5,解:作DG∥AC交BE的延长线于G, 则∠BDG=∠C=45°,又∠EDB=
则∠BDG=∠C=45°,又∠EDB= ![]() ∠C,∴∠EDB=∠EDG,在△EDB和△EDG中,
∠C,∴∠EDB=∠EDG,在△EDB和△EDG中, ,∴△EDB≌△EDG,∴BE=EG=
,∴△EDB≌△EDG,∴BE=EG= ![]() BG,∵∠BDG=∠C=45°,∴HB=HD,∵∠BEF=∠DHF=90°,∴∠HBG=∠HDF,在△BHG和△DHF中,
BG,∵∠BDG=∠C=45°,∴HB=HD,∵∠BEF=∠DHF=90°,∴∠HBG=∠HDF,在△BHG和△DHF中, ,∴△BHG≌△DHF,∴DF=BG,∴BE=
,∴△BHG≌△DHF,∴DF=BG,∴BE= ![]() FD
FD
(2)解:由(1)得,BE=EG= ![]() BG,
BG,
∵DG∥AC,
∴ ![]() =
= ![]() =k,
=k,
∵∠HBG=∠HDF,∠BHG=∠DHF=90°,
∴△BHG∽△DHF,
∴ ![]() =
= ![]() =k,
=k,
∴ ![]() =
= ![]()
【解析】解:(1)①∵∠A=90°,AB=AC,
∴∠ABC=∠C=45°,
∴∠EDB= ![]() ∠C=22.5°,又BE⊥DE,
∠C=22.5°,又BE⊥DE,
∴∠EBD=90°﹣22.5°=67.5°,
∴∠EBF=67.5°﹣45°=22.5°,
所以答案是:22.5;
【考点精析】关于本题考查的等腰三角形的性质和相似三角形的判定与性质,需要了解等腰三角形的两个底角相等(简称:等边对等角);相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能得出正确答案.

 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案【题目】中华文明,源远流长;中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
成绩x/分 | 频数 | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | 40 | n |
80≤x<90 | m | 0.35 |
90≤x≤100 | 50 | 0.25 |
请根据所给信息,解答下列问题:
(1)m= ,n= ;
(2)请补全频数分布直方图;
(3)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等约有多少人?