ЬтФПФкШн
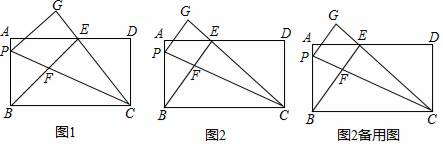
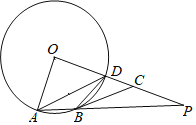
ЁОЬтФПЁПШчЭМЃЌвбжЊЕШБпЁїAOCЕФжмГЄЮЊ3ЃЌзїODЁЭACгкЕуDЃЌдкxжсЩЯШЁЕуC1ЃЌЪЙCC1ЃНDCЃЌвдCC1ЮЊБпзїЕШБпЁїA1CC1ЃЛзїCD1ЁЭA1C1гкЕуD1ЃЌдкxжсЩЯШЁЕуC2ЃЌЪЙC1C2ЃНD1C1ЃЌвдC1C2ЮЊБпзїЕШБпЁїA2C1C2ЃЛзїC1D2ЁЭA2C2гкЕуD2ЃЌдкxжсЩЯШЁЕуCЃЌЪЙC2C3ЃНD2C2ЃЌвдC2C3ЮЊБпзїЕШБпЁїA3C2C3ЃЛЁЃЌЧвЕуAЃЌA1ЃЌA2ЃЌA3ЃЌЁЖМдкЕквЛЯѓЯоЃЌШчДЫЯТШЅЃЌдђЕШБпЁїA2019C2018C2019ЕФЖЅЕуA2019зјБъЮЊ_____ЃЎ

ЁОД№АИЁП(![]() ЃЌ
ЃЌ![]() )
)
ЁОНтЮіЁП
ИљОнЕШБпШ§НЧаЮЕФаджЪЗжБ№ЧѓГіC1C2ЃЌC2C3ЃЌC3C4ЃЌЁЃЌCnCn+1ЕФБпГЄМДПЩНтОіЮЪЬтЃЎ
ЁпЕШБпЁїA1C1C2ЕФжмГЄЮЊ3ЃЌODЁЭACгкЕуDЃЌ
ЁрOCЃН1ЃЌC1C2ЃНCDЃН![]() OCЃН
OCЃН![]() ЃЌ
ЃЌ
ЁрOCЃЌCC1ЃЌC1C2ЃЌC2C3ЃЌЁЃЌC2018C2019ЕФГЄЗжБ№ЮЊ1ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЁЃЌ
ЃЌЁЃЌ![]() ЃЌ
ЃЌ
OC2019ЃНOC+CC1+C1C2+C2C3ЃЌЁ+C2018C2019ЃН1+![]() +
+![]() +
+![]() +Ё+
+Ё+![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЕШБпЁїA2019C2018C2019ЖЅЕуA2019ЕФКсзјБъЃН![]() Љ
Љ![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЕШБпЁїA2019C2018C2019ЖЅЕуA2019ЕФзнзјБъЃН![]() ЁС
ЁС![]() ЃН
ЃН![]() ЃЎ
ЃЎ
ЙЪД№АИЮЊЃК(![]() ЃЌ
ЃЌ![]() )ЃЎ
)ЃЎ

СЗЯАВсЯЕСаД№АИ
 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
ЯрЙиЬтФП