��Ŀ����
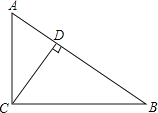
����Ŀ����ͼ1����A��B��C�ֱ��ǡ�O�ϲ��غϵ����㣬����AC��BC.
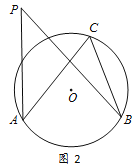
��1����ͼ2����P��ֱ��AB�Ϸ����ڡ�O�������һ�㣬 ����AP��BP.�ԱȽϡ�APB���ACB�Ĵ�С��ϵ����˵�����ɣ�
��2�� ����P�ǡ�O������һ�㣬 ����AP��BP���Ƚϡ�APB���ACB��С��ϵ��
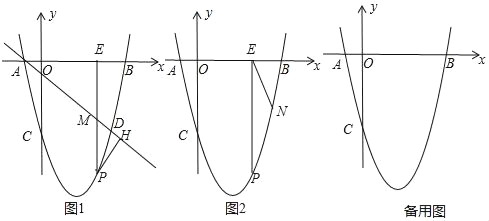
��3����ͼ3����ƽ��ֱ������ϵxOy�У���A���B������ֱ��ǣ�1��0������5��0������P��ֱ��y����x��һ���㣬����APBȡ�����ֵʱ��ֱ��д����P�����꣬����Ҫ˵����P��λ�������ȷ���ģ�


���𰸡���1����APB����ACB����2����APB����ACB����3��![]() .
.
��������
��1����AP���O���ڵ�E������AE������Բ�ܽǶ�����֪��AEB=��ACB��������������ǵ����ʿɵá�AEB����APB���ɴ˿ɵó����ۣ�
��2����BP���ӳ������O���ڵ�D������AD������Բ�ܽǶ�����֪��D=��C��������������ǵ����ʿɵ���D����APB���ɴ˿ɵó����ۣ�
��3������������ǵ����ʿ�֤�ã���ͬԲ���Բ�У�ͬ�����Ե�Բ�ܽǴ���ͬ�����Ե�Բ��ǣ�Ҫ��APB���ֻ�蹹�����A����B����ֱ��y����x���е�Բ���е����ʹ�á�APB���ĵ�P��Ȼ�������ߵ����ʡ���������ǵ����ʡ����ɶ�����֪ʶ���ɽ�����⣮
��1����APB����ACB
��ͼ��������PB��AB�Ϸ�Բ���ڵ�E������AE.
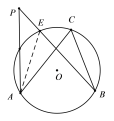
�� ��AEB����PAE�����
�� ��AEB����APB
���� ��AEB=��ACB
�� ��APB����ACB
��2����APB����ACB��
��ͼ�У��ӳ�BP��Բ�ڵ�D������AD��
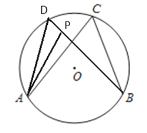
�ߡ�D=��C��
�֡ߡ�D����APB��
���APB����ACB��
��3��![]() ,
,
���߶�AB�Ĵ�ֱƽ��������һ��Q�����Ե�QΪԲ�ġ�QAΪ�뾶��Բ��ֱ��y=��x�����ڵ�������ʱ�����е㼴Ϊ��Ҫȷ���ĵ�P��λ��.
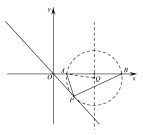
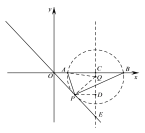
��ͼ����Q��ֱ���ڵ�P����AB�Ĵ�ֱƽ����CQ.
��CQ�ij�Ϊx����������֪��OA=1��OC=CE=3��
��QE=3��x��QD=![]() ��
��
��![]()
Rt��AQC��![]() ,
,
��![]() ,
,
��ã�![]() ����Ȼ��P�ڵ������ޱ��ڵڶ�����ʱ��APB����,
����Ȼ��P�ڵ������ޱ��ڵڶ�����ʱ��APB����,
��![]() ,
,
��![]() ,
,
��P![]() .
.