题目内容
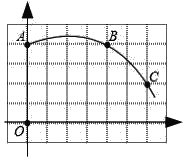
【题目】如图,网格纸中每个小正方形的边长为1,一段圆弧经过格点,点O为坐标原点.
(1)该图中弧所在圆的圆心D的坐标为 ;.
(2)根据(1)中的条件填空:
①圆D的半径= (结果保留根号);
②点(7,0)在圆D (填“上”、“内”或“外”);
③∠ADC的度数为 .
【答案】(1)(2,0);(2)①![]() ;②外;③90°;
;②外;③90°;
【解析】
根据垂径定理的推论:弦的垂直平分线必过圆心,可以作弦AB和BC的垂直平分线,交点即为圆心,根据勾股定理即可得到圆的半径;根据点到圆心的距离d=5即可判断点与圆的位置关系.
解:(1)根据垂径定理的推论:弦的垂直平分线必过圆心,
可以作弦AB和BC的垂直平分线,交点即为圆心.
如图所示,
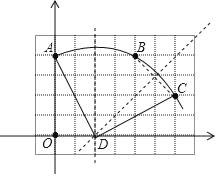
则圆心D的坐标为(2,0);
(2)①圆D的半径=![]() =2
=2![]() ,
,
②∵点(7,0)到圆心的距离d=5,
∴d>r,故该点在圆D外;
③如图,由A(0,4), C(6,2)可知,∠ADC的度数为90°.
故答案为:(2,0),2![]() ,外,90°.
,外,90°.

练习册系列答案
相关题目