Question

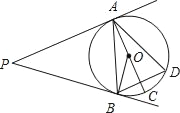
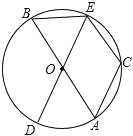
【题目】如图，在⊙O中，AB、DE为⊙O的直径，C是⊙O上一点，且=．

（1）BE与CE有什么数量关系？为什么？

（2）若∠BOE=60°，则四边形OACE是什么特殊的四边形？请说明理由．

Answer 1

【答案】（1）BE=CE，证明见解析；（2）四边形OACE是菱形，证明见解析；

【解析】

（1）根据对顶角相等得到∠AOD=∠BOE，再根据圆心角、弧、弦的关系得 ，加上 ，所以，于是有BE=CE；
（2）连结OC可得△COE和△AOC是等边三角形，可得四边形OACE的四条边都相等，再根据菱形的判定即可求解．

（1）∵AB、DE是⊙O的直径，

∴∠AOD=∠BOE，

∴，

∵，

∴，

∴BE=CE．

（2）连结OC，

∵∠BOE=60°，BE=CE，

∴∠COE=60°，

∵OC=OE，

∴△COE是等边三角形，

∵∠AOC=180°﹣60°﹣60°=60°，OA=OC，

∴△AOC是等边三角形，

∴OE=CE=OA=AC=OC，

∴四边形OACE是菱形．