题目内容
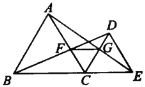
【题目】图1、图2中,点B为线段AE上一点,△ABC与△BED都是等边三角形.
(1)如图1,求证:AD=CE.
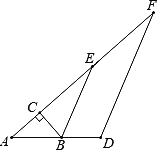
(2)如图2,设CE与AD交于点F,连接BF.
①求证:∠CFA=60°.
②求证:CF+BF=AF.

【答案】(1)证明见解析;(2)①证明见解析;②证明见解析.
【解析】
(1)如图1,利用等边三角形性质得:BD=BE,AB=BC,∠ABC=∠DBE=60°,再证∠ABD=∠CBE,根据SAS证明△ABD≌△CBE得出结论;
(2)①如图2,利用(1)中的全等得:∠BCE=∠DAB,根据两次运用外角定理可得结论;
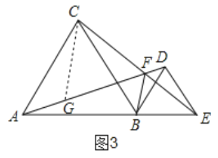
②如图3,作辅助线,截取FG=CF,连接CG,证明△CFG是等边三角形,并证明△ACG≌△BCF,由线段的和得出结论.
证明:(1)如图1,∵△ABC与△BED都是等边三角形,
∴BD=BE,AB=BC,∠ABC=∠DBE=60°,
∴∠ABC+∠CBD=∠DBE+∠CBD,
即∠ABD=∠CBE,
∴△ABD≌△CBE(SAS),
∴AD=CE,
(2)①如图2,由(1)得:△ABD≌△CBE,
∴∠BCE=∠DAB,
∵∠ABC=∠BCE+∠CEB=60°,
∴∠ABC=∠DAB+∠CEB=60°,
∵∠CFA=∠DAB+∠CEB,
∴∠CFA=60°,
②如图3,在AF上取一点G,使FG=CF,连接CG,
∵∠AFC=60°,
∴△CGF是等边三角形,
∴∠GCF=60°,CG=CF,
∴∠GCB+∠BCE=60°,
∵∠ACB=60°,
∴∠ACG+∠GCB=60°,
∴∠ACG=∠BCE,
∵AC=BC,
∴△ACG≌△BCF,
∴AG=BF,
∵AF=AG+GF,
∴AF=BF+CF.

练习册系列答案
相关题目