题目内容
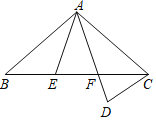
【题目】如图,反比例函数![]() (k≠0)的图象经过点A(1,2)和B(2,n),
(k≠0)的图象经过点A(1,2)和B(2,n),
(1)以原点O为位似中心画出△A1B1O,使![]() =
=![]() ;
;
(2)在y轴上是否存在点P,使得PA+PB的值最小?若存在,求出P的坐标;若不存在,请说明理由.

【答案】(1)作图见解析;(2)存在,P(0,![]() ).
).
【解析】
(1)有两种情形,分别画出图象即可;
(2)存在.如图作点A关于y轴的对称点A′,连接BA′交y轴于P,连接PA,此时PA+PB的值最小.求出直线BA′的解析式即可解决问题.
(1)△A1B1O的图象如图所示.
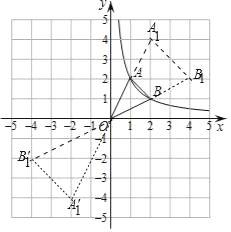
(2)存在.如图作点A关于y轴的对称点A′,连接BA′交y轴于P,连接PA,此时PA+PB的值最小.
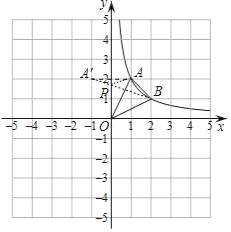
∵点A(1,2)在反比例函数y=![]() 上,
上,
∴k=2,
∴B(2,1),
∵A′(﹣1,2),
设最小BA′的解析式为y=kx+b,则有![]() ,
,
解得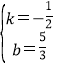 ,
,
∴直线BA′的解析式为y=﹣![]() x+
x+![]() ,
,
∴P(0,![]() ).
).

练习册系列答案
相关题目
【题目】某公园门票的收费标准如下:
门票类别 | 成人票 | 儿童票 | 团体票(限5张及以上) |
价格(元/人) | 100 | 40 | 60 |
有两个家庭分别去该公园游玩,每个家庭都有5名成员,且他们都选择了最省钱的方案购买门票,结果一家比另一家少花40元,则花费较少的一家花了( )元.
A.300B.260C.240D.220