题目内容
如图,∠AOB=120°,OD平分∠BOC,OE平分∠AOC。
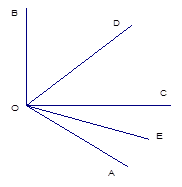
①求∠EOD的度数。②若∠BOC=90°,求∠AOE的度数。

①求∠EOD的度数。②若∠BOC=90°,求∠AOE的度数。
①∠EOD=60° ②∠AOE=15°
分析:OD、OE分别平分∠BOC、∠AOC,可得∠EOD=∠EOC+∠COD=1/2∠AOB,进而得到∠EOD的度数。
解答:
∵OD、OE分别平分∠BOC、∠AOC,
∴∠BOD=∠COD=1/2∠BOC,∠AOE=∠EOC=1/2∠AOC,
∵∠AOB=120°,
∴∠EOD=∠COD+∠EOC=1/2(∠BOC+∠AOC)=1/2∠AOB=60°。
故∠EOD的度数为60°。
∵∠BOC=90°,
∴∠AOE=1/2∠AOC=1/2(∠AOB-∠BOC)=1/2(120°-90°)=15°。
点评:本题考查角与角之间的运算,注意结合图形,发现角与角之间的关系,进而求解。

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目

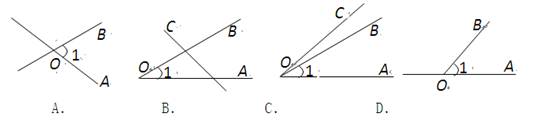
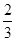 还少40º,求这个角.
还少40º,求这个角.

 AOB,点M、N.
AOB,点M、N.