题目内容
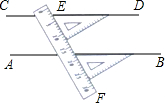
如图,O是直线AB上一点,OC为任一条射线,OD平分∠BOC, OE平分∠AOC.试说明∠COD与∠COE具有怎样的数量关系.

∠COD+∠COE=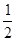 ∠AOB=90°
∠AOB=90°
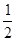 ∠AOB=90°
∠AOB=90°∠COD+∠COE=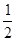 ∠AOB=90°。(提示:因为OD平分∠BOC,
∠AOB=90°。(提示:因为OD平分∠BOC,
所以∠COD=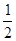 ∠BOC。
∠BOC。
又OE平分∠AOC,所以∠COE=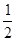 ∠AOC,
∠AOC,
所以∠COD+∠COE=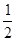 ∠BOC+
∠BOC+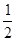 ∠AOC=
∠AOC=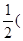 ∠BOC+∠AOC),
∠BOC+∠AOC),
所以∠COD+∠COE=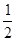 ∠AOB=90°。
∠AOB=90°。
结合图形,根据余角、补角的定义,有时还需考虑角平分线的性质,分析并找到角与角之间的关系,再进行计算得出答案
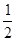 ∠AOB=90°。(提示:因为OD平分∠BOC,
∠AOB=90°。(提示:因为OD平分∠BOC,所以∠COD=
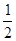 ∠BOC。
∠BOC。又OE平分∠AOC,所以∠COE=
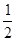 ∠AOC,
∠AOC,所以∠COD+∠COE=
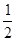 ∠BOC+
∠BOC+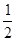 ∠AOC=
∠AOC=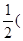 ∠BOC+∠AOC),
∠BOC+∠AOC),所以∠COD+∠COE=
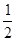 ∠AOB=90°。
∠AOB=90°。结合图形,根据余角、补角的定义,有时还需考虑角平分线的性质,分析并找到角与角之间的关系,再进行计算得出答案

练习册系列答案
相关题目
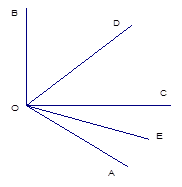
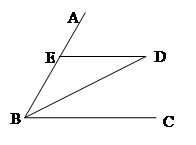
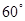 方向走了
方向走了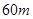 到达A点,再从A点沿着北偏西
到达A点,再从A点沿着北偏西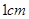 代表
代表 ,画出示意图,并量出示意图中线段BO的长度.
,画出示意图,并量出示意图中线段BO的长度.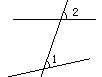
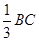 ,求CE的长。
,求CE的长。