题目内容
如图所示,点C、D为线段AB的三等分点,点E为线段AC的中点,若ED=9,求线段AB的长度.


因为C、D为线段AB的三等分点
所以AC=CD=DB
又因为点E为AC的中点,则AE=EC=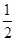 AC
AC
所以,CD+EC="DB+AE"
因为ED=EC+CD=9 所以, DB+AE=" EC+CD" =ED=9
则AB=2ED=18.
或者设EC=x,则AC=CD=DB=2x,AB=6x,
因为ED=9,则有x+2x=9,解得x=3,
则AB=6x=6×3=18
所以AC=CD=DB
又因为点E为AC的中点,则AE=EC=
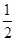 AC
AC 所以,CD+EC="DB+AE"
因为ED=EC+CD=9 所以, DB+AE=" EC+CD" =ED=9
则AB=2ED=18.
或者设EC=x,则AC=CD=DB=2x,AB=6x,
因为ED=9,则有x+2x=9,解得x=3,
则AB=6x=6×3=18
根据点C、D为线段AB的三等分点,点E为线段AC的中点,找出各线段之间的关系,即可求解。

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案
相关题目


 方向走了
方向走了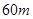 到达A点,再从A点沿着北偏西
到达A点,再从A点沿着北偏西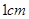 代表
代表 ,画出示意图,并量出示意图中线段BO的长度.
,画出示意图,并量出示意图中线段BO的长度.