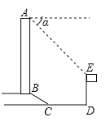
题目内容
【题目】如图,在![]() 中,
中,![]() 为斜边
为斜边![]() 中点,点P从A出发,沿
中点,点P从A出发,沿![]() 以每秒5个单位的速度向终点B运动,过点P作
以每秒5个单位的速度向终点B运动,过点P作![]() 于F,得到矩形
于F,得到矩形![]() 与矩形
与矩形![]() 的一边交于点G,连接PC,设点P的运动时间为
的一边交于点G,连接PC,设点P的运动时间为![]() 秒.
秒.
(1)求线段![]() 的长(用含
的长(用含![]() 的代数式表示);
的代数式表示);
(2)当![]() 时,求线段
时,求线段![]() 多长;
多长;
(3)当点P不与![]() 重合时,设矩形
重合时,设矩形![]() 与三角形CPD重叠部分图形的面积是
与三角形CPD重叠部分图形的面积是![]() ,求
,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(4)在点P出发的同时,点Q从点D出发,沿![]() 以每秒6个单位的速度向终点D移动,当点Q在矩形
以每秒6个单位的速度向终点D移动,当点Q在矩形![]() 内部时,直接写出
内部时,直接写出![]() 的取值范围.
的取值范围.
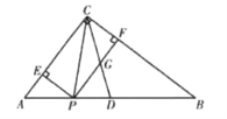
【答案】(1)![]() ;(2)3;(3)
;(2)3;(3) ;(4)当
;(4)当![]() 时,且
时,且![]()
【解析】
(1)根据矩形的性质CF=EP,在三角形AEP中,利用三角函数比表示出EP即可;
(2))当![]() 时,求出AP和PD的长度,再证
时,求出AP和PD的长度,再证![]() ,利用相似比可得出PG的长度;
,利用相似比可得出PG的长度;
(3)分类讨论,当P点在AD上运动时或当P点在BD上运动时,通过相似三角形,用t的代数式表示出三角形CPG的面积即可;
(4)取几个极限位置点,Q点在PE和在PF上,及与C点重合的时候,算出t的值,综合起来确定t的取值范围即可;
(1)如图1,在三角形ABC中,![]()
![]()
![]()
![]()
![]()
![]() ,
,
![]()
![]()
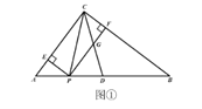
(2)如图1,当![]() 时,
时, ![]()
![]()
因为四边形PECF是矩形
所以![]()
![]()
![]()
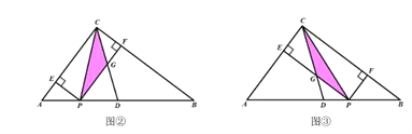
(3)当P点在AD上运动时,即![]() 时,如图②可得:
时,如图②可得:
![]() ,
,![]()
![]()
当P点在DB上运动时,即![]() 时,如图③可得:
时,如图③可得:
![]() ,
,![]()
![]()
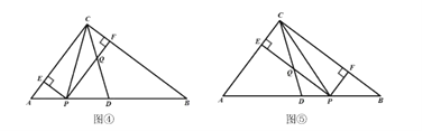
(4)
当点Q落在PF上时,如图④,有![]() ;
;
当点Q与点C重合时,![]() ;
;
当点Q落在PE上时,如图⑤时,![]() ,
,
综上可得,t的取值范围是:![]() ,且
,且![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目