题目内容
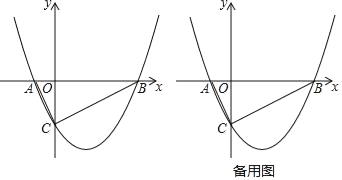
【题目】已知二次函数y＝x2－2mx＋m2＋m－1（m是常数）．
（1）求证：不论m为何值，该函数的图像的顶点都在函数y＝x－1的图像上．
（2）若该函数的图像与函数y＝x＋b的图像有两个交点，则b的取值范围为（ ）
A．b＞0 B．b＞－1 C．b＞－
D．b＞－2
（3）该函数图像与坐标轴交点的个数随m的值变化而变化，直接写出交点个数及对应的m的取值范围．
【答案】（1）详见解析；（2）C；（3）①当m＞1时，该函数图像与坐标轴交点的个数为1；②m＝1，
，
时，该函数图像与坐标轴交点的个数为2；③当m＜
，＜m＜
，＜m＜1时，该函数图像与坐标轴交点的个数为3．
【解析】
（1）首先求出抛物线的顶点坐标，然后代入直线解析式进行判断即可；
（2）联立方程组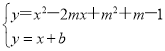
，根据方程组有两组解，利用根的判别式进行判断即可；
（3）分别由当抛物线的顶点在直线y=x-1与x轴的交点上方时，抛物线与坐标轴有一个交点，抛物线顶点在x轴上以及抛物线经过原点时，抛物线与坐标轴有2个交点分别列式求出m的值即可确定答案．
（1）证明：∵y＝x2－2mx＋m2＋m－1
＝(x－m)2＋m－1
∴该函数的图像的顶点坐标为（m，m－1），
将x＝m代入y＝x－1得，y＝m－1，
∴不论m为何值，该函数的图像的顶点都在函数y＝x－1的图像上．
（2）联立方程组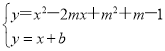
∴x2－2mx＋m2＋m－1=x＋b
整理，得：x2－（2m+1）x＋m2＋m－1-b=0
∵函数y＝x2－2mx＋m2＋m－1的图像与函数y＝x＋b的图像有两个交点，
∴△=
解得，b＞－
故选：C．
（3）∵该函数的图像的顶点坐标为（m，m－1），
①当m-1＞0，即m＞1时，该函数图像与y轴有一个交点，
∴当m＞1时，该函数图像与坐标轴交点的个数为1；
②当函数的图像的顶点在x轴以及经过原点时，
由于函数的图像的顶点在函数y＝x－1的图像上
∴当y=0时，x=1，即m=；
当图象经过原点时，即m2＋m－1=0，
解得，
， 
∴当m＝1，，时，该函数图像与坐标轴交点的个数为2；
③当m＜，＜m＜，＜m＜1时，该函数图像与坐标轴交点的个数为3．
