题目内容
【题目】如图,根据图中数据完成填空,再按要求答题:
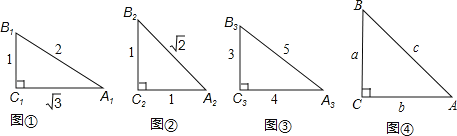
sin2A1+sin2B1= ;sin2A2+sin2B2= ;sin2A3+sin2B3= .
(1)观察上述等式,猜想:在Rt△ABC中,∠C=90°,都有sin2A+sin2B= .
(2)如图④,在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别是a、b、c,利用三角函数的定义和勾股定理,证明你的猜想.
【答案】(1)1;(2)证明见解析.
【解析】
试题分析:(1)由前面的结论,即可猜想出:在Rt△ABC中,∠C=90°,都有sin2A+sin2B=1;
(2)在Rt△ABC中,∠C=90°.利用锐角三角函数的定义得出sinA=![]() ,sinB=
,sinB=![]() ,则sin2A+sin2B=
,则sin2A+sin2B=![]() ,再根据勾股定理得到a2+b2=c2,从而证明sin2A+sin2B=1;
,再根据勾股定理得到a2+b2=c2,从而证明sin2A+sin2B=1;
试题解析:(1)由图可知:sin2A1+sin2B1=(![]() )2+(
)2+(![]() )2=1;
)2=1;
sin2A2+sin2B2=(![]() )2+(
)2+(![]() )2=1;
)2=1;
sin2A3+sin2B3=(![]() )2+(
)2+(![]() )2=1.
)2=1.
观察上述等式,可猜想:sin2A+sin2B=1.
(2)如图,在Rt△ABC中,∠C=90°.
∵sinA=![]() ,sinB=
,sinB=![]() ,
,
∴sin2A+sin2B=![]() ,
,
∵∠C=90°,
∴a2+b2=c2,
∴sin2A+sin2B=1.

练习册系列答案
相关题目
