题目内容
【题目】抛物线![]() 的顶点为A,抛物线
的顶点为A,抛物线![]() 的顶点为B,其中m≠﹣2,抛物线
的顶点为B,其中m≠﹣2,抛物线![]() 与
与![]() 相交于点P.
相交于点P.
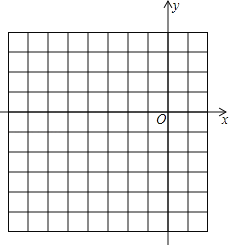
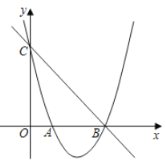
(1)当m=﹣3时,在所给的平面直角坐标系中画出C1,C2的图象;
(2)已知点C(﹣2,1),求证:点A,B,C三点共线;
(3)设点P的纵坐标为q,求q的取值范围.
【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】
(1)先将![]() 代入求出两条抛物线的解析式,再列表描点、顺次连接即可得出图象;
代入求出两条抛物线的解析式,再列表描点、顺次连接即可得出图象;
(2)先根据抛物线的解析式求出点A、B的坐标,再求出A和B所在直线的解析式,最后将点C的坐标代入直线解析式,判断其是否在直线上即可;
(3)联立两条抛物线的解析式,求出点P的坐标,从而可得q是含m的代数式,再根据二次函数的性质求解即可.
(1)当![]() 时
时
抛物线![]() ,列表如下:
,列表如下:
x |
| ﹣5 | ﹣4 | ﹣3 | ﹣2 | ﹣1 |
|
y |
| ﹣4 | ﹣1 | 0 | ﹣1 | ﹣4 |
|
抛物线![]() ,列表如下:
,列表如下:
x |
| ﹣3 | ﹣2 | ﹣1 | 0 | 1 |
|
y |
| ﹣2 | 1 | 2 | 1 | ﹣2 |
|
在平面直角坐标系中描点、顺次连接得出![]() 的图象如图所示:
的图象如图所示:

(2)∵抛物线![]() 化成顶点式为
化成顶点式为![]()
∴顶点A的坐标为![]()
由抛物线![]() 得点B的坐标为
得点B的坐标为![]()
设直线AB解析式为![]()
将![]() 代入
代入![]() 得:
得:

![]() 得:
得:![]() ,即
,即![]()
![]()
![]()
把![]() 代入①得:
代入①得:![]()
∴直线AB解析式为![]()
当![]() 时,
时,![]()
则![]() 在直线AB上,即点A,B,C三点共线;
在直线AB上,即点A,B,C三点共线;
(3)联立两条抛物线的解析式得:
![]() 得:
得:![]()
整理得:![]()
提取公因式得:![]()
![]()
![]()
把![]() 代入③得:
代入③得:![]()
则点P的坐标为![]()
因此,![]()
由二次函数的性质可知:当![]() 时,q随m的增大而增大;当
时,q随m的增大而增大;当![]() 时,q随m的增大而减小
时,q随m的增大而减小
则当![]() 时,q取得最大值
时,q取得最大值![]() ,所以
,所以![]()
又由于![]() ,所以q不能取
,所以q不能取![]()
故q的取值范围为![]() .
.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目