题目内容
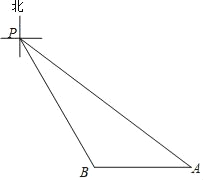
【题目】如图,P点是某海域内的一座灯塔的位置,船A停泊在灯塔P的南偏东53°方向的50海里处,船B位于船A的正西方向且与灯塔P相距20![]() 海里.(本题参考数据sin53°≈0.80,cos53°≈0.60,tan53°≈1.33.)
海里.(本题参考数据sin53°≈0.80,cos53°≈0.60,tan53°≈1.33.)
(1)试问船B在灯塔P的什么方向?
(2)求两船相距多少海里?(结果保留根号)
【答案】(1)船B在灯塔P的南偏东30°的方向上;(2)两船相距(40﹣10![]() )海里.
)海里.
【解析】
(1)过过P作PC⊥AB交AB于C,在Rt△APC中,利用余弦的定义求出PC=30海里,在Rt△PBC中,利用余弦定义可求出cos∠BPC=![]() ,从而求出∠BPC=30°;
,从而求出∠BPC=30°;
(2) 在Rt△APC中,利用正弦函数求出AC=40海里,在Rt△PBC中,根据30°角所对的直角边等于斜边的一半可求出BC=10![]() ,进而可求出AB的值
,进而可求出AB的值
(1)过P作PC⊥AB交AB于C,
在Rt△APC中,∠C=90°,∠APC=53°,AP=50海里,
∴PC=APcos53°=50×0.60=30海里,
在Rt△PBC中,∵PB=20![]() ,PC=30,
,PC=30,
∴cos∠BPC=![]() =
=![]() ,
,
∴∠BPC=30°,
∴船B在灯塔P的南偏东30°的方向上;
(2)∵AC=APsin53°=50×0.8=40海里,
BC=![]() PB=10
PB=10![]() ,
,
∴AB=AC﹣BC=(40﹣10![]() )海里,
)海里,
答:两船相距(40﹣10![]() )海里.
)海里.

【题目】某市射击队甲、乙两名队员在相同的条件下各射耙10次,每次射耙的成绩情况如图所示:
(1)请将下表补充完整:(参考公式:方差S2=![]() [(x1﹣
[(x1﹣![]() )2+(x2﹣
)2+(x2﹣![]() )2+…+(xn﹣
)2+…+(xn﹣![]() )2])
)2])
平均数 | 方差 | 中位数 | |
甲 | 7 |
| 7 |
乙 |
| 5.4 |
|
(2)请从下列三个不同的角度对这次测试结果进行
①从平均数和方差相结合看, 的成绩好些;
②从平均数和中位数相结合看, 的成绩好些;
③若其他队选手最好成绩在9环左右,现要选一人参赛,你认为选谁参加,并说明理由.