ЬтФПФкШн
ЁОЬтФПЁПвбжЊШчЭМЃКХзЮяЯп![]() гы
гы![]() жсНЛгк
жсНЛгк![]() СНЕуЃЈЕу
СНЕуЃЈЕу![]() дкЕу
дкЕу![]() ЕФзѓВрЃЉгы
ЕФзѓВрЃЉгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌЕу
ЃЌЕу![]() ЮЊХзЮяЯпЕФЖЅЕуЃЌЙ§Еу
ЮЊХзЮяЯпЕФЖЅЕуЃЌЙ§Еу![]() ЕФЖдГЦжсНЛ
ЕФЖдГЦжсНЛ![]() жсгкЕу
жсгкЕу![]() .
.
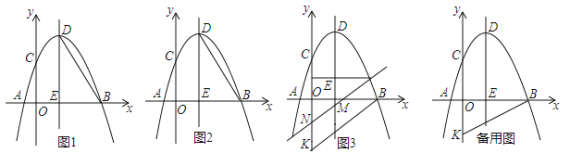
ЃЈ1ЃЉШчЭМ1ЃЌСЌНг![]() ЃЌЪдЧѓГіжБЯп
ЃЌЪдЧѓГіжБЯп![]() ЕФНтЮіЪНЃЛ
ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЕу![]() ЮЊХзЮяЯпЕквЛЯѓЯоЩЯвЛЖЏЕуЃЌСЌНг
ЮЊХзЮяЯпЕквЛЯѓЯоЩЯвЛЖЏЕуЃЌСЌНг![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЕБЫФБпаЮ
ЃЌЕБЫФБпаЮ![]() ЕФУцЛ§зюДѓЪБЃЌЯпЖЮ
ЕФУцЛ§зюДѓЪБЃЌЯпЖЮ![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌЧѓДЫЪБ
ЃЌЧѓДЫЪБ![]() :
:![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌвбжЊЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌНЋ
ЃЌНЋ![]() бизХ
бизХ![]() жсЩЯЯТЦНвЦЃЈАќРЈ
жсЩЯЯТЦНвЦЃЈАќРЈ![]() ЃЉдкЦНвЦЕФЙ§ГЬжажБЯп
ЃЉдкЦНвЦЕФЙ§ГЬжажБЯп![]() НЛ
НЛ![]() жсгкЕу
жсгкЕу![]() ЃЌНЛ
ЃЌНЛ![]() жсгкЕу
жсгкЕу![]() ЃЌдђдкХзЮяЯпЕФЖдГЦжсЩЯЪЧЗёДцдкЕу
ЃЌдђдкХзЮяЯпЕФЖдГЦжсЩЯЪЧЗёДцдкЕу![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЪЧвд
ЪЧвд![]() ЮЊжБНЧБпЕФЕШбќжБНЧШ§НЧаЮЃЌШєДцдкЃЌЧыжБНгаДГіЕу
ЮЊжБНЧБпЕФЕШбќжБНЧШ§НЧаЮЃЌШєДцдкЃЌЧыжБНгаДГіЕу![]() ЕФзјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЕФзјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЁОД№АИЁПЃЈ1ЃЉy=-![]() x+
x+![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉG1ЃЈ2ЃЌ
ЃЛЃЈ3ЃЉG1ЃЈ2ЃЌ![]() ЃЉ,G2ЃЈ2ЃЌ-7ЃЉЃЌG3ЃЈ2ЃЌ-3ЃЉG4ЃЈ2ЃЌ-
ЃЉ,G2ЃЈ2ЃЌ-7ЃЉЃЌG3ЃЈ2ЃЌ-3ЃЉG4ЃЈ2ЃЌ-![]() ЃЉ
ЃЉ
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКЃЈ1ЃЉИљОнздБфСПгыКЏЪ§жЕЕФЖдгІЙиЯЕЃЌПЩЕУAЁЂBЕузјБъЃЌИљОнЖЅЕузјБъЕФЖЈвхЃЌПЩЕУDЕузјБъЃЌИљОнД§ЖЈЯЕЪ§ЗЈЃЌПЩЕУД№АИЃЛ
ЃЈ2ЃЉИљОнЦНаагкBCЧвгыХзЮяЯпЯрЧаЃЌПЩЕУЙ§PЕуЦНааBCЕФжБЯпЃЌИљОнНтЗНГЬзщЃЌПЩЕУPЕузјБъЃЌИљОнНтЗНГЬзщЃЌПЩЕУFЕузјБъЃЌИљОнЯрЫЦШ§НЧаЮЕФаджЪЃЌПЩЕУД№АИЃЛ
ЃЈ3ЃЉИљОнЦНвЦЕФаджЪЃЌПЩЕУжБЯпMNЕФНтЮіЪНЃЌИљОнШЋЕШШ§НЧаЮЕФХаЖЈгыаджЪЃЌПЩЕУЙигкbЕФЗНГЬЃЌИљОнНтЗНГЬЃЌПЩЕУbЃЌИљОнbЕФжЕЃЌПЩЕУOMЕФГЄЃЌПЩЕУEGЕФГЄЃЌПЩЕУД№АИЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉдкy=-![]() x2+2x+
x2+2x+![]() жаЃЌ
жаЃЌ
Сюy=0ЃЌдђ-![]() x2+2x+
x2+2x+![]() =0ЃЌ
=0ЃЌ
НтЕУЃКx1=-1ЃЎx2=5ЃЌ
дђAЕФзјБъЪЧЃЈ-1ЃЌ0ЃЉЃЌBЕФзјБъЪЧЃЈ5ЃЌ0ЃЉЃЎ
ХзЮяЯпy=-![]() x2+2x+
x2+2x+![]() ЕФЖдГЦжсЪЧx=2ЃЌ
ЕФЖдГЦжсЪЧx=2ЃЌ
Абx=2ДњШыНтЮіЪНЕУy=![]() ЃЌдђDЕФзјБъЪЧЃЈ2ЃЌ
ЃЌдђDЕФзјБъЪЧЃЈ2ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
ЩшжБЯпBDЕФНтЮіЪНЪЧy=kx+bЃЌ
ИљОнЬтвтЕУЃК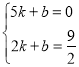 ЃЌ
ЃЌ
НтЕУЃК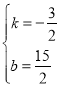 ЃЌ
ЃЌ
дђжБЯпBDЕФНтЮіЪНЪЧy=-![]() x+
x+![]() ЃЛ
ЃЛ
ЃЈ2ЃЉСЌНгBCЃЌШчЭМ2ЃЌ
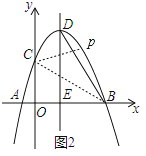
y=-![]() x2+2x+
x2+2x+![]() жаЃЌСюx=0ЃЌдђy=
жаЃЌСюx=0ЃЌдђy=![]() ЃЌдђCЕФзјБъЪЧЃЈ0ЃЌ
ЃЌдђCЕФзјБъЪЧЃЈ0ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
ЩшBCЕФНтЮіЪНЪЧy=mx+nЃЌ
дђ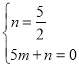 ЃЌ
ЃЌ
НтЕУЃК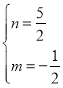 ЃЌ
ЃЌ
дђжБЯпBCЕФНтЮіЪНЪЧy=-![]() x+
x+![]() ЃЎ
ЃЎ
ЩшгыBCЦНааЧвгыХзЮяЯпжЛгавЛИіЙЋЙВЕуЕФжБЯпЕФНтЮіЪНЪЧy=-![]() x+dЃЎ
x+dЃЎ
дђ-![]() x2+2x+
x2+2x+![]() =-
=-![]() x+dЃЌ
x+dЃЌ
МДx2-5x+ЃЈ2d-10ЃЉ=0ЃЌ
ЕБЁї=0ЪБЃЌx=![]() ЃЌ
ЃЌ
ДњШыy=-![]() x2+2x+
x2+2x+![]() жаЕУЃКy=
жаЕУЃКy=![]() ЃЌ
ЃЌ
дђPЕФзјБъЪЧЃЈ![]() ЃЌ
ЃЌ ![]() ЃЉЃЎ
ЃЉЃЎ
гжЁпCЕФзјБъЪЧЃЈ0ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЩшCPЕФНтЮіЪНЪЧy=ex+fЃЌдђ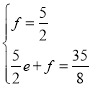
НтЕУЃК ЃЌ
ЃЌ
дђжБЯпCPЕФНтЮіЪНЪЧy=![]() x+
x+![]() ЃЎ
ЃЎ
ИљОнЬтвтЕУЃК ЃЌ
ЃЌ
НтЕУЃК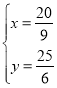 ЃЌ
ЃЌ
дђFЕФзјБъЪЧЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
дђ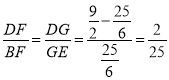 ЃЛ
ЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌ
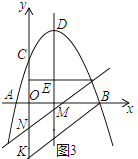
ЩшBKЕФНтЮіЪНЪЧy=kx+bЃЌ
дђ![]() ЃЌ
ЃЌ
НтЕУЃК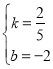 ЃЌ
ЃЌ
дђжБЯпBKЕФНтЮіЪНЪЧy=![]() x-2ЃЌ
x-2ЃЌ
MNЕФНтЮіЪНЮЊy=![]() x+bЃЌ
x+bЃЌ
ЕБy=0ЪБЃЌx=-![]() bЃЌМДMЃЈ-
bЃЌМДMЃЈ-![]() bЃЌ0ЃЉЃЌME=-
bЃЌ0ЃЉЃЌME=-![]() b-2ЃЎ
b-2ЃЎ
ЕБx=0ЪБЃЌy=bЃЌМДNЃЈ0ЃЌbЃЉЃЎ
гЩЁїGMNЪЧвдMNЮЊбќЕФЕШбќжБНЧШ§НЧаЮЃЌЕУ
MG=MNЃЌЁЯGMN=90ЁуЃЎ
ЁпЁЯMGE+ЁЯGME=90ЁуЃЌЁЯGME+ЁЯEMN=90ЁуЃЌ
ЁрЁЯMGE=ЁЯAMNЃЎ
дкЁїGMEКЭЁїMNAжаЃЌ
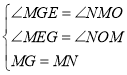 ЃЌ
ЃЌ
ЁрЁїGMEЁеЁїMNOЃЈAASЃЉЃЌ
ЁрME=ONЃЌEG=OMЃЌ
МД-![]() b-2=-bЃЎ
b-2=-bЃЎ
НтЕУb=-![]() ЃЎ
ЃЎ
EG=OM=-![]() b=
b=![]() ЃЌ
ЃЌ
G1ЕуЕФзјБъЮЊЃЈ2ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
ЭЌРэПЩЧѓЃКG2ЃЈ2ЃЌ-7ЃЉЃЌG3ЃЈ2ЃЌ-3ЃЉG4ЃЈ2ЃЌ-![]() ЃЉ
ЃЉ

 ЦЗбЇЫЋгХОэЯЕСаД№АИ
ЦЗбЇЫЋгХОэЯЕСаД№АИ аЁбЇЦкФЉГхДЬ100ЗжЯЕСаД№АИ
аЁбЇЦкФЉГхДЬ100ЗжЯЕСаД№АИ ЦкФЉИДЯАМьВтЯЕСаД№АИ
ЦкФЉИДЯАМьВтЯЕСаД№АИ ГЌФмбЇЕфЕЅдЊЦкжаЦкФЉзЈЬтГхДЬ100ЗжЯЕСаД№АИ
ГЌФмбЇЕфЕЅдЊЦкжаЦкФЉзЈЬтГхДЬ100ЗжЯЕСаД№АИ