题目内容
【题目】如图,直线y=﹣x+1与x轴,y轴分别交于B,A两点,动点P在线段AB上移动,以P为顶点作∠OPQ=45°交x轴于点Q.

(1)求点A和点B的坐标;
(2)比较∠AOP与∠BPQ的大小,说明理由.
(3)是否存在点P,使得△OPQ是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
【答案】(1)A(0,1),B(1,0);(2)∠AOP=∠BPQ,理由详见解析;(3)点P坐标为(0,1),(![]() )或(1
)或(1![]() )时,△OPQ是等腰三角形.
)时,△OPQ是等腰三角形.
【解析】
(1)根据直线y=﹣x+1即可求得A、B的坐标;
(2)根据OA=OB,求得△AOB是等腰直角三角形,得出∠OAB=∠OBA=45°,根据三角形外角的性质即可得出结论.
(3)假设存在等腰三角形,分三种情况讨论:(ⅰ)OP=OQ;(ⅱ)QP=QO;(ⅲ)PO=PQ.能求出P点坐标,则存在点P,否则,不存在.
(1)∵直线y=﹣x+1与x轴,y轴分别交于A,B两点,令x=0,则y=0+1=1,∴A(0,1),令y=0,则0=﹣x+1,解得:x=1,∴B(1,0).
(2)∠AOP=∠BPQ.理由如下:
∵A(0,1),B(1,0),∴OA=OB=1,∴∠OAB=∠OBA=45°.
∵∠OAP+∠AOP=∠OPB=∠OPQ+∠BPQ,∴45°+∠AOP=45°+∠BPQ,∴∠AOP=∠BPQ.
(3)△OPQ可以是等腰三角形.理由如下:
如图,过P点PE⊥OA交OA于点E.分三种情况讨论:
(ⅰ)若OP=OQ,则∠OPQ=∠OQP,∴∠POQ=90°,∴点P与点A重合,∴点P坐标为(0,1);
(ⅱ)若QP=QO,则∠OPQ=∠QOP=45°,所以PQ⊥QO,可设P(x,x)代入y=﹣x+1得x![]() ,∴点P坐标为(
,∴点P坐标为(![]() );
);
(ⅲ)若PO=PQ.
∵∠OPQ+∠1=∠2+∠3,而∠OPQ=∠3=45°,∴∠1=∠2.
又∵∠3=∠4=45°,∴△AOP≌△BPQ(AAS),PB=OA=1,∴AP![]() 1.
1.
由勾股定理求得:PE=AE=1![]() ,∴EO
,∴EO![]() ,∴点P坐标为(1
,∴点P坐标为(1![]() ).
).
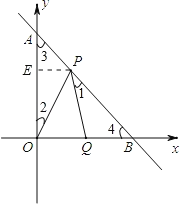
综上所述:点P坐标为(0,1),(![]() )或(1
)或(1![]() )时,△OPQ是等腰三角形.
)时,△OPQ是等腰三角形.

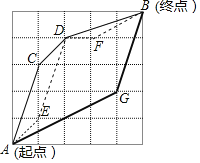
【题目】嘉嘉参加机器人设计活动,需操控机器人在5×5的棋盘格上从A点行走至B点,且每个小方格皆为正方形,主办单位规定了三条行走路径R1,R2,R2,其行经位置如图与表所示:
路径 | 编号 | 图例 | 行径位置 |
第一条路径 | R1 | … | A→C→D→B |
第二条路径 | R2 | … | A→E→D→F→B |
第三条路径 | R3 | … | A→G→B |
已知A,B,C,D,E,F,G七点皆落在格线的交点上,且两点之间的路径皆为线段.
(1)分别计算出三条路径的长;
(2)最长的路径是______ (写出编号),最短的路径是 _______(写出编号).