题目内容
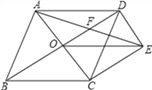
【题目】用若干块如左图所示的正方形或长方形纸片拼成图（1）和图（2）
（1）如图（1），若AD=7，AB=8，求
与
的值；
（2）如图（1），若长方形ABCD的面积为35，其中阴影部分的面积为20，求长方形ABCD的周长；
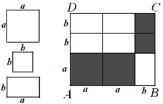
图（1）
（3）如图（2），若AD的长度为5，AB的长度为
．
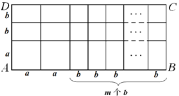
图（2）
①当
=________，=_________时，，的值有无数组；
②当________，_________时，，的值不存在．
【答案】(1) a=3，b=2； (2) C=24；（3）① m=4,n=10；② m=4,n≠10.
【解析】
（1）根据图（1）长方形ABCD的边长组成列方程即可解答；
（2）由图（1）中空白部分面积=大长方形面积-阴影部分面积=5个小长方形面积，可得ab=3，再结合完全平方公式可得（a+b）2=16，即可得a+b=4，而长方形ABCD的周长=2（3a+3b），由此即可解答；
（3）由长方形的长和宽可列出关于a、b的方程组，解关于a、b即可解答.
解：（1）由图得
，
解得：
，
（2）由图可得：5个小长方形面积=长方形ABCD的面积-阴影部分的面积，
∴
，
∴ab=3，
∵阴影部分的面积为20，
∴
，
∴
，
∴a+b=
，
方形ABCD的周长=2[(2a+b)+(2b+a)]=6（a+b）=6×4=24.
（3）由图（2）得：
，
由①得a=5-2b，③
将③代入②得2（5-2b）+mb=n，
∴（m-4）b=n-10，
∴当
时，a，b的解有无数组；
即m=4，n=10时，a，b的值有无数组；
当
时，方程组无解，
即m=4，n≠10时，a，b的值不存在.
故答案为：①m=4，n=10；②m=4，n≠10
【题目】为了对某市区全民阅读状况进行调查和评估，有关部门随机抽取了部分市民进行每天阅读时间情况的调查，并根据调查结果制做了如下尚不完整的频数分布表（被调查者每天的阅读时间均在0﹣120分钟之内）
阅读时间x（分钟） | 0≤x＜30 | 30≤x＜60 | 60≤x＜90 | 90≤x≤120 |
频数 | 450 | 400 | m | 50 |
频率 | 0.45 | 0.4 | 0.1 | n |
（1）被调查的市民人数为多少，表格中，m，n为多少；
（2）补全频数分布直方图；
（3）某市区目前的常住人口约有118万人，请估计该市区每天阅读时间在60～120分钟的市民大约有多少万人？
【题目】我市某中学决定在学生中开展丢沙包、打篮球、跳大绳和踢毽球四种项目的活动，为了解学生对四种项目的喜欢情况，随机调查了该校m名学生最喜欢的一种项目（每名学生必选且只能选择四种活动项目的一种），并将调查结果绘制成如下的不完整的统计图表：
学生最喜欢的活动项目的人数统计表
项目 | 学生数（名） | 百分比 |
丢沙包 | 20 | 10% |
打篮球 | 60 | p% |
跳大绳 | n | 40% |
踢毽球 | 40 | 20% |
根据图表中提供的信息，解答下列问题：
（1）m= ， n= ， p=；
（2）请根据以上信息直接补全条形统计图；
（3）根据抽样调查结果，请你估计该校2000名学生中有多少名学生最喜欢跳大绳．
