题目内容
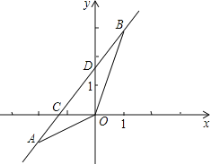
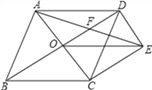
【题目】如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=![]() AC,连接AE交OD于点F,连接CE、OE.
AC,连接AE交OD于点F,连接CE、OE.
(1)求证:OE=CD;
(2)若菱形ABCD的边长为2,∠ABC=60°,求AE的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】分析:(1)由菱形ABCD中,DE∥AC且DE=![]() AC,易证得四边形OCED是平行四边形,继而可得OE=CD即可;
AC,易证得四边形OCED是平行四边形,继而可得OE=CD即可;
(2)由菱形的对角线互相垂直,可证得四边形OCED是矩形,根据菱形的性质得出AC=AB,再根据勾股定理得出AE的长度即可.
本题解析:
(1)证明:四边形ABCD是菱形,
∴OA=OC=![]() AC,AD=CD,
AC,AD=CD,
∵DE∥AC且DE=![]() AC,
AC,
∴DE=OA=OC,
∴四边形OADE、四边形OCED都是平行四边形,
(2)解:∵AC⊥BD,
∴OE=AD,
∴OE=CD;
∴四边形OCED是矩形,
∵在菱形ABCD中,∠ABC=60°,
∴AC=AB=2,
∴在矩形OCED中,CE=OD=![]() .
.
∴在Rt△ACE中,AE=![]() .
.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
【题目】列方程解应用题:五莲县新玛特购物中心第一次用5000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的![]() 倍多15件,甲、乙两种商品的进价和售价如下表(注:获利=售价﹣进价)
倍多15件,甲、乙两种商品的进价和售价如下表(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 20 | 30 |
售价(元/件) | 29 | 40 |
(1)新玛特购物中心将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(2)该购物中心第二次以第一次的进价又购进甲、乙两种商品,其中甲种商品的件数不变,乙种商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得总利润比第一次获得的总利润多160元,求第二次乙种商品是按原价打几折销售?