题目内容
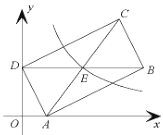
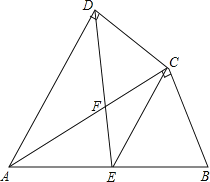
【题目】如图，在平行四边形ABCD中，P是AB边上的任意一点，过P点作PE⊥AB，交AD于E，连结CE、CP．已知∠A=60o ．
（1）试探究，当△CPE≌△CPB时，CD与DE的数量关系；
（2）若BC=4，AB=3，当AP的长为多少时，△CPE的面积最大，并求出面积的最大值．
【答案】（1）DE=DC；（2）AP=
；△CPE的面积最大，值为
．
【解析】
（1）由△CPE≌△CPB，根据全等三角形的对应边相等，对应角相等可得BC=CE，∠B=∠PEC=120°，进而得出∠ECD=∠CE D，再利用等角对等边得到ED=CD；
（2）延长PE交CD的延长线于F，设AP=x，OCPE的面积为y，由四边形ABCD为平行四边形可得AB=DC，AD=BC；在直角三角形APE中，可得∠PEA=30°；再利用直角三角形的性质表示出AE与PE;再由DE =AD-AE，再根据对顶角相等可得∠DEF=30°，利用直角三角形的性质可以表示出DF，进一步说明∠F=90°，再表示出三角形CPE的面积，得到y与x的函数解析式，最后利用二次函数的性质即可确定三角形CPE面积的最大值和AP的长．
（1）当△CPE≌△CPB时，有BC=CE，∠B=∠PEC=120°，
∴∠CED=180°-∠AEP-∠PEC=30°，
∵∠ADC=120°，
∴∠ECD=∠CED=180°-120°-30°=30°，
∴DE=CD
（2）延长PE交CD的延长线于F，设AP=x，△CPE的面积为y
∵四边形ABCD为平行四边形，
∴DC = AB =3，AD=BC=4，
∵Rt△APE，∠A=60°，
∴∠PEA=30°。
∴AE=2x，PE=
x，
在Rt△DEF中，∠DEF=∠PEA=30°，DE=AD-AE=4-2x，
∴DF=
DE=2-x，
∵AB//CD.PF⊥AB，
∴PF⊥CD，
∴
= PE·CF，即y=
，
配方得：y=
x（0≤x≤3），，
∴当x=，△CPE的面积有最大值为，即AP的长为时，OCPE的面积最大，最大面积是．
