题目内容
【题目】如图,平行四边形![]() 中,
中,![]() 和
和![]() 的平分线交于AD边上一点E,且
的平分线交于AD边上一点E,且![]() ,
,![]() ,则AB的长是( )
,则AB的长是( )
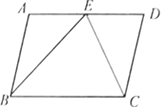
A. 2.5B. 3C. 4D. 2.4
【答案】A
【解析】
根据平行四边形的性质可证明△BEC是直角三角形,利用勾股定理可求出BC的长,利用角平分线的性质以及平行线的性质得出∠ABE=∠AEB,∠DEC=∠DCE,进而利用平行四边形对边相等进而得出答案.
∵四边形ABCD是平行四边形,∠ABC、∠BCD的角平分线的交点E落在AD边上,
∴∠ABE=∠EBC,∠DCE=∠ECB,AD//BC,AB//CD,
∴∠AEB=∠EBC,∠DEC=∠ECB,
∴∠ABE=∠AEB,∠DEC=∠DCE,
∴AB=AE,DE=DC,
∵AB//CD,
∴∠ABE+∠EBC+∠DCE+∠ECB=180°,
∴∠EBC+∠ECB=90°,
∴∠BEC=90°,
又∵BE=4,CE=3,
∴BC=![]() =5,
=5,
由题意可得:AB=CD,AD=BC,
∴AB=AE=![]() ,
,
故选A.

练习册系列答案
相关题目
【题目】已知△A′B′C′是由△ABC经过平移得到的,它们各顶点在平面直角坐标系中的坐标如下表所示:
△ABC | A(a,0) | B(3,0) | C(5,5) |
△A′B′C′ | A′(4,2) | B′(7,b) | C′(c,7) |
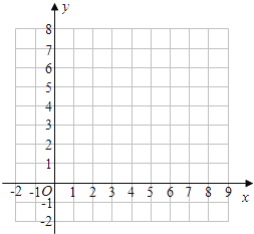
(1)观察表中各对应点坐标的变化,并填空:a=________,b=________,c=________;
(2)在平面直角坐标系中画出△ABC及平移后的△A′B′C′;
(3)直接写出△A′B′C′的面积是________.