题目内容
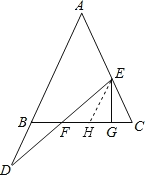
【题目】如图,在△ABC中,AB=AC,E在线段AC上,D在AB的延长线,连DE交BC于F,过点E作EG⊥BC于G.
(1)若∠A=50°,∠D=30°,求∠GEF的度数;
(2)若BD=CE,求证:FG=BF+CG.

【答案】(1)55°;(2)见解析
【解析】
(1)根据等腰三角形两底角相等及三角形内角和定理求出∠C,再根据直角三角形两锐角互余求出∠CEG,然后根据三角形的外角的性质求出∠CEF,即可得到结论;
(2)过点E作EH∥AB交BC于H,根据平行线的性质可得∠ABC=∠EHC,∠D=∠FEH,然后求出∠EHC=∠C,再根据等角对等边可得EC=EH,得出BD=EH,再利用“角角边”证明△BDF和△HEF全等,根据全等三角形对应边相等可得BF=FH,根据等腰三角形三线合一的性质可得CG=HG,即可得到结论.
(1)∵∠A=50°,∴∠C![]() (180°﹣∠A)
(180°﹣∠A)![]() (180°﹣50°)=65°.
(180°﹣50°)=65°.
∵EG⊥BC,∴∠CEG=90°﹣∠C=90°﹣65°=25°.
∵∠A=50°,∠D=30°,∴∠CEF=∠A+∠D=50°+30°=80°,∴∠GEF=∠CEF﹣∠CEG=80°﹣25°=55°;
(2)过点E作EH∥AB交BC于H,则∠ABC=∠EHC,∠D=∠FEH.
∵AB=AC,∴∠ABC=∠C,∴∠EHC=∠C,∴EC=EH.
∵BD=CE,∴BD=EH.
在△BDF和△HEF中,∵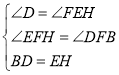 ,∴△BDF≌△HEF(AAS),∴BF=FH.
,∴△BDF≌△HEF(AAS),∴BF=FH.
又∵EC=EH,EG⊥BC,∴CG=HG,∴FG=FH+HG=BF+CG.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目