题目内容
【题目】在△ABC中,D是BC边上的点(不与点B、C重合),连结AD. 
(1)如图1,当点D是BC边上的中点时,S△ABD:S△ACD=;
(2)如图2,当AD是∠BAC的平分线时,若AB=m,AC=n,求S△ABD:S△ACD的值(用含m,n的代数式表示)
(3)如图3,AD平分∠BAC,延长AD到E,使得AD=DE,连接BE,如果AC=2,AB=4,S△BDE=6,那么S△ABC= .
【答案】
(1)1:1
(2)解:

过D作DE⊥AB于E,DF⊥AC于F,
∵AD为∠BAC的角平分线,
∴DE=DF,
∵AB=m,AC=n,
∴SABD:S△ACD=( ![]() ×AB×DE):(
×AB×DE):( ![]() ×AC×DF)=m:n
×AC×DF)=m:n
(3)9
【解析】解:(1) 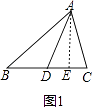
过A作AE⊥BC于E,
∵点D是BC边上的中点,
∴BD=DC,
∴SABD:S△ACD=( ![]() ×BD×AE):(
×BD×AE):( ![]() ×CD×AE)=1:1,
×CD×AE)=1:1,
所以答案是:1:1;
3)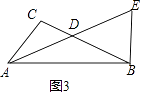
∵AD=DE,
∴由(1)知:S△ABD:S△EBD=1:1,
∵S△BDE=6,
∴S△ABD=6,
∵AC=2,AB=4,AD平分∠CAB,
∴由(2)知:S△ABD:S△ACD=AB:AC=4:2=2:1,
∴S△ACD=3,
∴S△ABC=3+6=9,
所以答案是:9.
【考点精析】解答此题的关键在于理解角平分线的性质定理的相关知识,掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上.

【题目】下表给出了代数式x2+bx+c与x的一些对应值:
x | … | 0 | 1 | 2 | 3 | 4 | … |
x2+bx+c | … | 3 | ﹣1 | 3 | … |
(1)请在表内的空格中填入适当的数;
(2)设y=x2+bx+c,则当x取何值时,y>0;
(3)请说明经过怎样平移函数y=x2+bx+c的图象得到函数y=x2的图象?



