题目内容
 已知正比例函数y=kx经过点A(2,1),如图所示.
已知正比例函数y=kx经过点A(2,1),如图所示.(1)求这个正比例函数的关系式.
(2)将这个正比例函数的图象向左平移4个单位,写出在这个平移下,点A、原点O的对应点A′、O′的坐标,求出平移后的直线O′A′所对应的函数关系式.
(3)已知点C的坐标为(-3,0),点P(x,y)为线段O′B上一动点(P与O′、B不重合),设△PCO的面积为S.
①求S与x之间的函数关系式及x的取值范围;
②求当S=
| 15 | 8 |
分析:(1)由于正比例函数y=kx经过点A(2,1),将点A(2,1)代入y=kx,求出k的值即可得到正比例函数解析式;
(2)由于点A、点O均向左平移4个单位,横坐标减2,纵坐标不变,求出A′、O′的坐标,再利用待定系数法求出函数解析式;
(3)①设P点坐标为(x,y),利用三角形面积公式即可求出S与x之间的函数关系式;
②令S=
,代入解析式S=
x+3,据此即可求出x的值,从而得到P的坐标.
(2)由于点A、点O均向左平移4个单位,横坐标减2,纵坐标不变,求出A′、O′的坐标,再利用待定系数法求出函数解析式;
(3)①设P点坐标为(x,y),利用三角形面积公式即可求出S与x之间的函数关系式;
②令S=
| 15 |
| 8 |
| 3 |
| 4 |
解答:解:(1)将点A(2,1)代入y=kx,得k=
,
故函数解析式为y=
x;
(2)∵正比例函数的图象向左平移4个单位,
∴点A、点O均向左平移4个单位,横坐标减2,纵坐标不变,
∴A′(-2,1),O′(-4,0).
设A′O′的解析式为y=kx+b,
将A′(-2,1),O′(-4,0)分别代入解析式,得
,
解得
,
故直线O′A′所对应的函数关系式为y=
x+2.
(3)①设P点坐标为(x,y),
则S=
•OC•y=
×3•y=
×3(
x+2)=
x+3(-3<x<0).
②当S=
时,
x+3=
,
解得x=-
,
将x=-
代入y=
x+2得,y=
×(-
)+2=-
+2=
,
则P点坐标为P(-
,
).
| 1 |
| 2 |
故函数解析式为y=
| 1 |
| 2 |
(2)∵正比例函数的图象向左平移4个单位,
∴点A、点O均向左平移4个单位,横坐标减2,纵坐标不变,
∴A′(-2,1),O′(-4,0).
设A′O′的解析式为y=kx+b,
将A′(-2,1),O′(-4,0)分别代入解析式,得
|
解得
|
故直线O′A′所对应的函数关系式为y=
| 1 |
| 2 |
(3)①设P点坐标为(x,y),
则S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
②当S=
| 15 |
| 8 |
| 3 |
| 4 |
| 15 |
| 8 |
解得x=-
| 3 |
| 2 |
将x=-
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 5 |
| 4 |
则P点坐标为P(-
| 3 |
| 2 |
| 5 |
| 4 |
点评:本题考查了一次函数综合题,设及待定系数法求函数解析式、三角形的面积、图形的平移等知识,是一道好题.

练习册系列答案
相关题目
已知正比例函数y=k1x(k1≠0)与反比例函数y=
(k2≠0)的图象有一个交点的坐标为(-2,-1),则它的另一个交点的坐标是( )
| k2 |
| x |
| A、(2,1) |
| B、(-2,-1) |
| C、(-2,1) |
| D、(2,-1) |
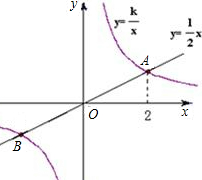 横坐标为2.
横坐标为2. 如图,已知正比例函数和反比例函数的图象都经过点A(3,3).
如图,已知正比例函数和反比例函数的图象都经过点A(3,3).