题目内容
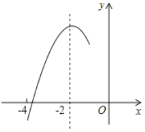
【题目】如图，抛物线
的对称轴为直线
，与
轴的一个交点在
和
之间，其部分图象如图所示．则下列结论：①
；②
；③
；④
（
为实数）；⑤点
，
，
是该抛物线上的点，则
，其中，正确结论的个数是（ ）
A.1B.2C.3D.4
【答案】C
【解析】
根据对称轴公式可得
，即可判断①；然后根据抛物线的对称轴和与x轴的交点坐标即可判断抛物线与
轴的另一个交点在
和
之间，从而判断②和③；由图象可得当x=-2时，y取最大值，最大值为
，从而判断④；最后利用抛物线的对称性和增减性即可判断⑤．
解：∵抛物线
的对称轴为直线
，
∴
解得：b=4a
∴
，故①正确；
∵抛物线与轴的一个交点在
和
之间，
∴抛物线与轴的另一个交点在和之间，
∴当x=0时，y＜0；当x=-1时，y＞0
∴当x=0时，y=c＜0，故②正确；
当x=-1时，y=a－b＋c＞0
∴a－4a＋c＞0
解得：
，故③错误；
由图象可得当x=-2时，y取最大值，最大值为
∴当x=t时，
≤
∴
，故④错误；
关于直线x=-2的对称点为
由抛物线可得当x＜-2时，y随x的增大而增大
∵
∴
，故⑤正确
综上：正确的结论有3个
故选C．
练习册系列答案
星级口算天天练系列答案
相关题目
【题目】去年5月份，我市某中学开展争做“五好小公民”征文比赛活动，赛后随机抽取了部分参赛学生的成绩，按得分划分为
，
，
，
四个等级，并绘制了如下不完整的频数分布表和扇形统计图：
等级 | 成绩（ | 频数（人数） |
|
| 6 |
|
|
|
|
| 24 |
|
| 9 |
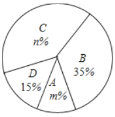
根据以上信息，解答以下问题：
（1）表中的
；
（2）扇形统计图中
，
，等级对应的扇形的圆心角为 度；
（3）该校准备从上述获得等级6名学生中选取两人做为学校“五好小公民”志愿者，已知这6人中有3名男生（用
，
，
表示）和3名女生（用
，
，
表示），请用列表或画树状图的方法求恰好选取的是和的概率．
