题目内容
在直角坐标系中,点A的坐标是(3,0),点P在第一象限内的直线y=-x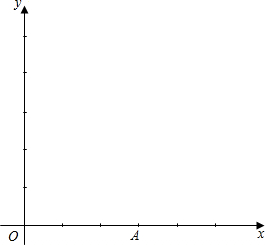 +4上.设点P的坐标为(x,y).
+4上.设点P的坐标为(x,y).(1)在所给的坐标系中画出直线y=-x+4;
(2)求△POA的面积S与变量x的函数关系式,并写出自变量x的取值范围;
(3)当S=
| 9 | 2 |
分析:(1)先求出直线y=-x+4x轴、y轴的交点,再根据题意画出直线y=-x+4即可;
(2)先写出△POA的面积S的表达式,在将其中的y替换成x的函数即可;
(3)先求出P点坐标,作出△POA,再以△POA两边垂直平分线的交点为圆心、圆心到任一顶点为半径,作圆,即为△POA的外接圆.
(2)先写出△POA的面积S的表达式,在将其中的y替换成x的函数即可;
(3)先求出P点坐标,作出△POA,再以△POA两边垂直平分线的交点为圆心、圆心到任一顶点为半径,作圆,即为△POA的外接圆.
解答: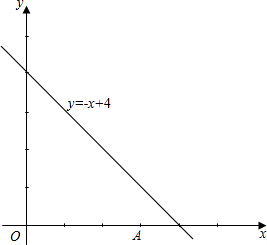 (本小题满分12分)
(本小题满分12分)
解:(1)直线y=-x+4分别交x轴、y轴于(4,0)(0,4);
如图所示:
(2)∵点P在第一象限,
∴点P的纵坐标y的绝对值|y|就是△POA的边OA上高的值,
∴S=
•OA•y=
y,即S=
y,
而点P为线段BC上一点,故y=-x+4,
∴S=
(-x+4)=-
x+6,
又而点P在线段BC上,自变量x的取值范围为:0<x<4
即所求S与变量x的函数关系式为: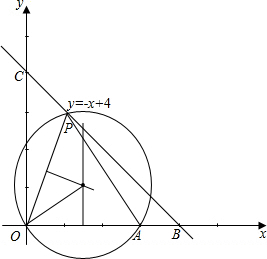
S=-
x+6(0<x<4),
(3)若S=
,则有
=
y,y=3,
代入y=-x+4,得x=1,
∴点P的坐标为(1,3),
用尺规分别作出△POA的OA、OP(或AP)边的垂直平分线,
以两线交点为圆心、圆心到任一顶点为半径,作圆,即为△POA的外接圆(图形略).【以图形为准给分,不必写作法】
 (本小题满分12分)
(本小题满分12分)解:(1)直线y=-x+4分别交x轴、y轴于(4,0)(0,4);
如图所示:
(2)∵点P在第一象限,
∴点P的纵坐标y的绝对值|y|就是△POA的边OA上高的值,
∴S=
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
而点P为线段BC上一点,故y=-x+4,
∴S=
| 3 |
| 2 |
| 3 |
| 2 |
又而点P在线段BC上,自变量x的取值范围为:0<x<4
即所求S与变量x的函数关系式为:
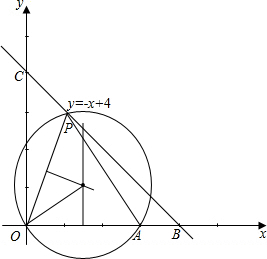
S=-
| 3 |
| 2 |
(3)若S=
| 9 |
| 2 |
| 9 |
| 2 |
| 3 |
| 2 |
代入y=-x+4,得x=1,
∴点P的坐标为(1,3),
用尺规分别作出△POA的OA、OP(或AP)边的垂直平分线,
以两线交点为圆心、圆心到任一顶点为半径,作圆,即为△POA的外接圆(图形略).【以图形为准给分,不必写作法】
点评:本题主要考查了一次函数的综合题,解答要注意数形结合思想的运用,是各地中考的热点,要求同学们作图规范,同学们要加强训练,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
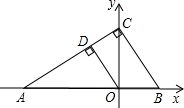 C作CB⊥AC,交x轴于B.
C作CB⊥AC,交x轴于B.