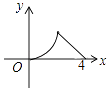��Ŀ����
����Ŀ����ͼ����������x�ύ��A��x1 �� 0����B��x2 �� 0�����㣬��x1��x2 �� ��y�ύ�ڵ�C��0����4��������x1 �� x2�Ƿ���x2��4x��12=0����������
��1���������ߵĽ���ʽ��
��2����M���߶�AB�ϵ�һ�����㣬����M��MN��BC����AC�ڵ�N������CM������CMN��������ʱ�����M�����ꣻ
��3����D��4��k���ڣ�1�����������ϣ���EΪ��������һ���㣬��x�����Ƿ���ڵ�F��ʹ��A��D��E��FΪ������ı�����ƽ���ı��Σ�������ڣ�����������������ĵ�F�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺��x2��4x��12=0��
��x1=��2��x2=6��
��A����2��0����B��6��0����
�֡������߹���A��B��C�����������ߵĽ���ʽΪy=a��x+2����x��6����
����C��������룬��� ![]() ��
��
�������ߵĽ���ʽΪ ![]() ��
��
��2��
�⣺���M������Ϊ��m��0��������N��NH��x���ڵ�H����ͼ��1������
�ߵ�A������Ϊ����2��0������B������Ϊ��6��0����
��AB=8��AM=m+2��
��MN��BC�����MNA�ס�BCA��
�� ![]() ��
��
�� ![]() ��
��
�� ![]() ��
��
�� ![]() ��
��
= ![]() ��
��
= ![]() ��
��
�൱m=2ʱ��S��CMN�����ֵ4��
��ʱ����M������Ϊ��2��0����

��3��
�⣺�ߵ�D��4��k���������� ![]() �ϣ�
�ϣ�
�൱x=4ʱ��k=��4��
���D�������ǣ�4����4����
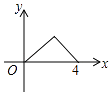
����ͼ��2������AFΪƽ���ı��εı�ʱ��AFƽ���ҵ���DE��

��D��4����4������DE=4��
��F1����6��0����F2��2��0����
����ͼ��3������AFΪƽ���ı��εĶԽ���ʱ����F��n��0����

�ߵ�A������Ϊ����2��0����
��ƽ���ı��εĶԳ����ĵĺ�����Ϊ�� ![]() ��
��
��ƽ���ı��εĶԳ���������Ϊ�� ![]() ��0����
��0����
��D��4����4����
��E'�ĺ�����Ϊ�� ![]() ��4+
��4+ ![]() =n��6��
=n��6��
E'����������4��
��E'��������n��6��4����
��E'��n��6��4������ ![]() ����n2��16n+36=0��
����n2��16n+36=0��
��� ![]() ��
�� ![]() ��
�� ![]() ��
��
��������F1����6��0����F2��2��0����F3��8��2 ![]() ��0����F4��8+2
��0����F4��8+2 ![]() ��0����
��0����
����������1������һԪ���η��̽ⷨ�ó�A��B��������꣬�����ý���ʽ������κ�������ʽ����2�������ж���MNA�ס�BCA���ó� ![]() �������ó���������ֵ����3���ֱ���ݵ�AFΪƽ���ı��εı�ʱ��AFƽ���ҵ���DE�뵱AFΪƽ���ı��εĶԽ���ʱ�������ó�����Ҫ��Ĵ𰸣�
�������ó���������ֵ����3���ֱ���ݵ�AFΪƽ���ı��εı�ʱ��AFƽ���ҵ���DE�뵱AFΪƽ���ı��εĶԽ���ʱ�������ó�����Ҫ��Ĵ𰸣�