题目内容
【题目】如图,△ABC是等腰直角三角形,∠A=90°,BC=4,点P是△ABC边上一动点,沿B→A→C的路径移动,过点P作PD⊥BC于点D,设BD=x,△BDP的面积为y,则下列能大致反映y与x函数关系的图象是( )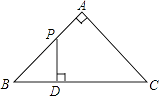
A.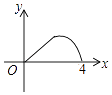
B.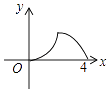
C.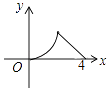
D.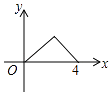
【答案】B
【解析】解:过A点作AH⊥BC于H,
∵△ABC是等腰直角三角形,
∴∠B=∠C=45°,BH=CH=AH= ![]() BC=2,
BC=2,
当0≤x≤2时,如图1,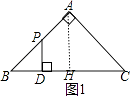
∵∠B=45°,
∴PD=BD=x,
∴y= ![]() xx=
xx= ![]() x2;
x2;
当2<x≤4时,如图2,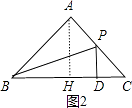
∵∠C=45°,
∴PD=CD=4﹣x,
∴y= ![]() (4﹣x)x=﹣
(4﹣x)x=﹣ ![]() x2+2x,
x2+2x,
故选B
过A点作AH⊥BC于H,利用等腰直角三角形的性质得到∠B=∠C=45°,BH=CH=AH= ![]() BC=2,分类讨论:当0≤x≤2时,如图1,易得PD=BD=x,根据三角形面积公式得到y=
BC=2,分类讨论:当0≤x≤2时,如图1,易得PD=BD=x,根据三角形面积公式得到y= ![]() x2;当2<x≤4时,如图2,易得PD=CD=4﹣x,根据三角形面积公式得到y=﹣
x2;当2<x≤4时,如图2,易得PD=CD=4﹣x,根据三角形面积公式得到y=﹣ ![]() x2+2x,于是可判断当0≤x≤2时,y与x的函数关系的图象为开口向上的抛物线的一部分,当2<x≤4时,y与x的函数关系的图象为开口向下的抛物线的一部分,然后利用此特征可对四个选项进行判断.
x2+2x,于是可判断当0≤x≤2时,y与x的函数关系的图象为开口向上的抛物线的一部分,当2<x≤4时,y与x的函数关系的图象为开口向下的抛物线的一部分,然后利用此特征可对四个选项进行判断.

【题目】为丰富学生的校园生活,某校举行“与爱同行”朗诵比赛,赛后整理参赛同学的成绩,绘制成如下不完整的统计图表,请根据图表中的信息解答下列问题.
组别 | 成绩x(分) | 频数(人数) |
A | 8.0≤x<8.5 | a |
B | 8.5≤x<9.0 | 8 |
C | 9.0≤x<9.5 | 15 |
D | 9.5≤x<10 | 3 |

(1)图中a= , 这次比赛成绩的众数落在组;
(2)请补全频数分布直方图;
(3)学校决定选派本次比赛成绩最好的3人参加全市中学生朗诵比赛,并为参赛选手准备了2件白色、1件蓝色上衣和黑色、蓝色、白色的裤子各1条,小军先选,他从中随机选取一件上衣和一条裤子搭配成一套衣服,请用画树状图法或列表法求出上衣和裤子搭配成不同颜色的概率.






