题目内容
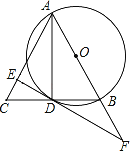
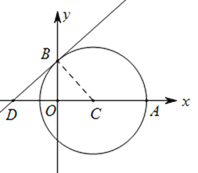
【题目】如图，在直角坐标系中，以点
为圆心，以3为半径的圆，分别交
轴正半轴于点
，交
轴正半轴于点
，过点的直线交轴负半轴于点
．
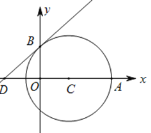
（1）求
两点的坐标；
（2）求证：直线
是⊙的切线．
【答案】（1）
,
；（2）详见解析．
【解析】
（1）先根据圆的半径可求出CA的长，再结合点C坐标即可得出点A坐标；根据点C坐标可知OC的长，又根据圆的半径可求出CB的长，然后利用勾股定理可求出OB的长，即可得出点B坐标；
（2）先根据点
坐标分别求出
，再根据勾股定理的逆定理可得
是直角三角形，然后根据圆的切线的判定定理即可得证．
（1）∵
，圆的半径为3
∴
，
∴
点A是x轴正半轴与圆的交点
∴
如图，连接CB，则
在
中，
点B是y轴正半轴与圆的交点
∴
；
（2）∵
∴
在
中，
则在中，
是直角三角形，即
又∵BC是⊙C半径
∴直线BD是⊙C的切线．
练习册系列答案
同步练习强化拓展系列答案
相关题目
【题目】某鱼塘中养了某种鱼5000条，为了估计该鱼塘中该种鱼的总质量，从鱼塘中捕捞了3次，取得的数据如下：
数量/条 | 平均每条鱼的质量/kg | |
第1次捕捞 | 20 | 1.6 |
第2次捕捞 | 15 | 2.0 |
第3次捕捞 | 15 | 1.8 |
（1）求样本中平均每条鱼的质量；
（2）估计鱼塘中该种鱼的总质量；
（3）设该种鱼每千克的售价为14元，求出售该种鱼的收入y（元）与出售该种鱼的质量x（kg）之间的函数关系，并估计自变量x的取值范围．
