题目内容
(1)解不等式组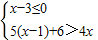 并把解集在数轴上表示出来;
并把解集在数轴上表示出来;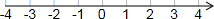
(2)如图,已知墙高AB为6.5米,将一长为6米的梯子CD斜靠在墙面,梯子与地面所成的角∠BCD=55°,此时梯子的顶端与墙顶的距离AD约为多少米?(结果精确到0.1米)(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)

【答案】分析:(1)先求出其中各不等式的解集,再求出这些解集的公共部分,然后利用数轴表示不等式组的解集即可;
(2)在Rt△BCD中,根据∠BCD=55°,CD=6米,解直角三角形求出BD的长度,继而可求得AD=AB-BD的长度.
解答:解:(1) ,
,
解不等式①得:x≤3,
解不等式②得,x>-1,
则不等式的解集为:-1<x≤3,
不等式组的解集在数轴上表示为:
 ;
;
(2)在Rt△BCD中,
∵∠DBC=90°,∠BCD=55°,CD=6米,
∴BD=CD×sin∠BCD=6×sin55°≈6×0.82=4.92(米),
∴AD=AB-BD≈6.5-4.92=1.58≈1.6(米).
答:梯子的顶端与墙顶的距离AD约为1.6米.
点评:(1)本题考查了解一元一次不等式组的知识,解答本题的关键是掌握一元一次不等式组的解法:先求出其中各不等式的解集,再求出这些解集的公共部分,然后利用数轴表示不等式组的解集即可;
(2)本题考查了解直角三角形的应用的知识,解答本题的关键是根据已知条件构造直角三角形并利用解直角三角形的知识求解,难度适中.
(2)在Rt△BCD中,根据∠BCD=55°,CD=6米,解直角三角形求出BD的长度,继而可求得AD=AB-BD的长度.
解答:解:(1)
 ,
,解不等式①得:x≤3,
解不等式②得,x>-1,
则不等式的解集为:-1<x≤3,
不等式组的解集在数轴上表示为:
 ;
;(2)在Rt△BCD中,
∵∠DBC=90°,∠BCD=55°,CD=6米,
∴BD=CD×sin∠BCD=6×sin55°≈6×0.82=4.92(米),
∴AD=AB-BD≈6.5-4.92=1.58≈1.6(米).
答:梯子的顶端与墙顶的距离AD约为1.6米.
点评:(1)本题考查了解一元一次不等式组的知识,解答本题的关键是掌握一元一次不等式组的解法:先求出其中各不等式的解集,再求出这些解集的公共部分,然后利用数轴表示不等式组的解集即可;
(2)本题考查了解直角三角形的应用的知识,解答本题的关键是根据已知条件构造直角三角形并利用解直角三角形的知识求解,难度适中.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目