题目内容
解不等式组并把解集在数轴上表示出来.(1)
|
(2)
|
(3)-7≤
| 2(1+3x) |
| 7 |
(4)
|
分析:先解不等式组中的每一个不等式,再把不等式的解集表示在数轴上,即可.解(4)不等式组中不等式时,先利用分数基本性质化小数分母为整数即2(x-3)-(5x+2)≤-14,再去括号,移项合并,为-3x≤-6,最后化系数为1时,两边同除以-3,不等号要改变方向,解集为x≥2.
解答:解:(1)原不等式组化简为
解不等式①得x>-2
解不等式②得x≤1
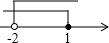
把不等式①②的解集在数轴上表示出来,因此不等式组的解集为-2<x≤1.
(2)
解:解不等式①得x<
解不等式②得x>-1
解不等式③得x≤2
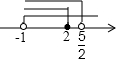
所以原不等式组的解集为-1<
x≤2.
(3)解:原不等式化为不等式组
化简为
解不等式①得x≥-
解不等式②得x≤
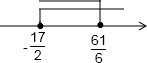
所以不等式组的解集为-
≤x≤
.
(4)解:原不等式组化简为
解不等式①得x<-3
解不等式②得x≥2
所以不等式组的解集为空集也即无解.
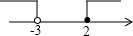
|
解不等式①得x>-2
解不等式②得x≤1
把不等式①②的解集在数轴上表示出来,因此不等式组的解集为-2<x≤1.

(2)
|
解:解不等式①得x<
| 5 |
| 2 |
解不等式②得x>-1
解不等式③得x≤2
所以原不等式组的解集为-1<
x≤2.

(3)解:原不等式化为不等式组
|
化简为
|
解不等式①得x≥-
| 17 |
| 2 |
解不等式②得x≤
| 61 |
| 6 |
所以不等式组的解集为-
| 17 |
| 2 |
| 61 |
| 6 |

(4)解:原不等式组化简为
|
解不等式①得x<-3
解不等式②得x≥2
所以不等式组的解集为空集也即无解.
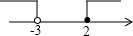
点评:不等式组的解集在数轴上表示的方法:把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目