题目内容
【题目】如图，等边
的周长为
，作
于
，在
的延长线取点
，使
，连接
，以
为边作等边
；作
于
，在的延长线上取点
，使
，连接
，以
为边作等边
；且点
都在直线同侧，如此下去，则
的周长为__________．（
，且
为整数）
【答案】
【解析】
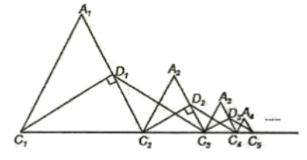
先根据等边三角形的性质得出D1C2=C2C3=
A1C2，进而根据已知得到△A2C2C3的周长=△A1C1C2的周长＝，从而推导出△AnCnCn+1的周长为.
∵△A1C1C2是等边三角形，C1D1⊥A1C2于D1，
∴A1D1＝D1C2＝A1G2，∠A1C2C1＝60°，
∴∠D1C1C2＝30°，
∵D1C3＝D1C1，
∴∠D1C1C2＝∠D1C3C2＝30°，
∴∠C2D1C3＝30°，
∴D1C2=C2C3=A1C2，
∵△A1C1C2的周长为1,
∴△A2C2C3的周长=△A1C1C2的周长＝，
……
∴△AnCnCn+1的周长为.
练习册系列答案
相关题目
【题目】某日王老师佩戴运动手环进行快走锻炼，两次锻炼后数据如表．与第一次锻炼相比，王老师第二次锻炼步数增长的百分率是其平均步长减少的百分率的3倍．设王老师第二次锻炼时平均步长减少的百分率为
．
项目 | 第一次锻炼 | 第二次锻炼 |
步数(步) | 10000 | ____________ |
平均步长(米/步) | 0.6 | ____________ |
距离(米) | 6000 | 7020 |
注：步数×平均步长＝距离．
(1)根据题意完成表格填空；
(2)求x；
(3)王老师发现好友中步数排名第一为24000步，因此在两次锻炼结束后又走了500米，使得总步数恰好为24000步，求王老师这500米的平均步长．
