Question

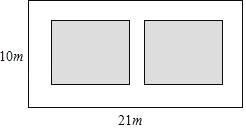
【题目】如图，有一块长为21m、宽为10m的矩形空地，计划在其中修建两块相同的矩形绿地，两块绿地之间及周边留有宽度相等的人行通道，且人行通道的宽度不能超过3米．

(1)如果两块绿地的面积之和为90m2，求人行通道的宽度；

(2)能否改变人行通道的宽度，使得每块绿地的宽与长之比等于3：5，请说明理由．

Answer 1

【答案】（1）2米；（2）不能改变人行横道的宽度使得每块绿地的宽与长之比等于3：5．

【解析】

（1）设人行通道的宽度为x米，将两块矩形绿地的长和宽用含有x的式子表示出来，根据“两块矩形绿地的面积共为90平方米”列出关于x的一元二次方程，解之即可；（2）根据每块绿地的宽与长之比等于3：5列出方程求得人行横道的宽度后与3米比较即可得到答案．

（1）设人行通道的宽度为x米，

则两块矩形绿地的长为（21﹣3x）（米），

宽为（10﹣2x）（米），

根据题意得：（21﹣3x）（10﹣2x）＝90，

解得：x1＝10（舍去），x2＝2，

答：人行通道的宽度为2米；

（2）设人行通道的宽为y米时，每块绿地的宽与长之比等于3：5，

根据题意得：（10﹣2y）：＝3：5，

解得：y＝，

∵＞3，

∴不能改变人行横道的宽度使得每块绿地的宽与长之比等于3：5．