题目内容
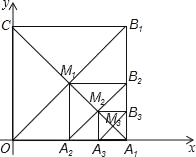
【题目】甲、乙两组工人同时开始加工某种零件,乙组在工作中有一次停产更换设备,更换设备后,乙组的工作效率是原来的2倍.两组各自加工零件的数量y(件)与时间x(时)之间的函数图象如图所示.甲、乙两组加工出的零件合在一起装箱,每够300件装一箱,零件装箱的时间忽略不计,求经过_____小时恰好装满第1箱.
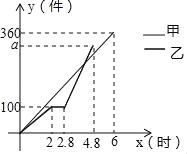
【答案】3
【解析】
根据工作效率=工作总量÷工作时间分别算出甲、乙组每小时加工零件数,结合函数图象找出y甲、y乙关于x(乙组在x≥2.8时间段)的函数关系式,令y甲+y乙=300求出x值,此题得解.
甲组每小时加工零件数为:360÷6=60(件),乙组停产前每小时加工零件数为:100÷2=50(件),乙组停产后每小时加工零件数为:50×2=100(件),∴甲组加工零件的数量y件与时间x之间的函数关系式为y甲=60x,乙组在x≥2.8时间段加工零件的数量y件与时间x之间的函数关系式为y乙=100x+b,将(2.8,100)代入y乙=100x+b中,100=2.8×100+b,解得:b=﹣180,∴乙组在x≥2.8时间段加工零件的数量y件与时间x之间的函数关系式为y乙=100x﹣180(x≥2.8).
令y甲+y乙=300,即60x+100x﹣180=300,解得:x=3.
故答案为:3.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目