题目内容
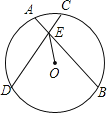
【题目】如图,⊙O的两条弦AB、CD交于点E,OE平分∠BED.
(1)求证:AB=CD;
(2)若∠BED=60°,EO=2,求DE﹣AE的值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题(1)过点O作AB、CD的垂线,垂足为M、N,由角平分线的性质,可得OM=ON,然后由弦心距相等可得弦相等,即AB=CD;
(2)由(1)可得,OM=ON,AB=CD,OM⊥AB,ON⊥CD,由垂径定理可得DN=CN=AM=BM,由HL可证Rt△EON≌Rt△EOM,继而可得NE=ME,
从而得AE=CE, DE-AE=DE-CE=DN+NE-CE=CN+NE-CE=2NE,在Rt△EON中,由∠NEO=30°,OE=2,即可求出NE.
试题解析:(1)过点O作AB、CD的垂线,垂足为M、N,如图1,


∵OE平分∠BED,且OM⊥AB,ON⊥CD,∴OM=ON,∴AB=CD;
(2)如图2所示,由(1)知,OM=ON,AB=CD,OM⊥AB,ON⊥CD,∴DN=CN=AM=BM,在Rt△EON与Rt△EOM中,∵![]() ,∴Rt△EON≌Rt△EOM(HL),∴NE=ME,∴CD﹣DN﹣NE=AB﹣BM﹣ME,即AE=CE,∴DE﹣AE=DE﹣CE=DN+NE﹣CE=CN+NE﹣CE=2NE,∵∠BED=60°,OE平分∠BED,∴∠NEO=
,∴Rt△EON≌Rt△EOM(HL),∴NE=ME,∴CD﹣DN﹣NE=AB﹣BM﹣ME,即AE=CE,∴DE﹣AE=DE﹣CE=DN+NE﹣CE=CN+NE﹣CE=2NE,∵∠BED=60°,OE平分∠BED,∴∠NEO= ![]() ∠BED=30°,∴ON=
∠BED=30°,∴ON=![]() OE=1,在Rt△EON中,由勾股定理得:NE=
OE=1,在Rt△EON中,由勾股定理得:NE=![]() =
=![]() ,∴DE﹣AE=2NE=2
,∴DE﹣AE=2NE=2![]() .
.

练习册系列答案
相关题目