题目内容
抛物线
![]() 交
交![]() 轴于
轴于![]() 、
、![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,顶点为
,顶点为![]() .
.

1.写出抛物线的对称轴及![]() 、
、![]() 两点的坐标(用含
两点的坐标(用含![]() 的代数式表示)
的代数式表示)
2.连接![]() 并以
并以![]() 为直径作⊙
为直径作⊙![]() ,当
,当![]() 时,请判断⊙
时,请判断⊙![]() 是否经过点
是否经过点![]() ,并说明理由;
,并说明理由;
3.在(2)题的条件下,点![]() 是抛物线上任意一点,过
是抛物线上任意一点,过![]() 作直线垂直于对称轴,垂足为
作直线垂直于对称轴,垂足为![]() . 那么是否存在这样的点
. 那么是否存在这样的点![]() ,使△
,使△![]() 与以
与以![]() 、
、![]() 、
、![]() 为顶点的三角形相似?若存在,请求出点
为顶点的三角形相似?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
1.过点C作CH⊥![]() 轴,垂足为H
轴,垂足为H
∵在Rt△OAB中,∠OAB=900,∠BOA=300,AB=2 ∴OB=4,OA=![]()
由折叠知,∠COB=300,OC=OA=![]()
∴∠COH=600,OH=![]() ,CH=3 ∴C点坐标为(
,CH=3 ∴C点坐标为(![]() ,3)
,3)
2.∵抛物线![]() (
(![]() ≠0)经过C(
≠0)经过C(![]() ,3)、A(
,3)、A(![]() ,0)两点
,0)两点
∴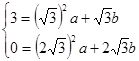 解得:
解得: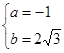
∴此抛物线的解析式为:![]() (7分)
(7分)
3.存在. 因为![]() 的顶点坐标为(
的顶点坐标为(![]() ,3)即为点C,MP⊥
,3)即为点C,MP⊥![]() 轴,设垂足为N,PN=
轴,设垂足为N,PN=![]() ,因为∠BOA=300,所以ON=
,因为∠BOA=300,所以ON=![]()
![]() , ∴P(
, ∴P(![]()
![]() ,
,![]() )
)
作PQ⊥CD,垂足为Q,ME⊥CD,垂足为E

把![]() 代入
代入![]() 得:
得:![]()
∴ M(![]()
![]() ,
,![]() ),E(
),E(![]() ,
,![]() )
)
同理:Q(![]() ,
,![]() ),D(
),D(![]() ,1)
,1)
要使四边形CDPM为等腰梯形,只需CE=QD
即![]() ,解得:
,解得:![]() ,
,![]() (舍)
(舍)
∴ P点坐标为(![]() ,
,![]() )
)
∴ 存在满足条件的点P,使得四边形CDPM为等腰梯形,此时P点的坐为(![]() ,
,![]() ) (12分)
) (12分)
解析:略

练习册系列答案
相关题目

 交
交 轴于
轴于 、
、 两点,交
两点,交 轴于点
轴于点 ,顶点为
,顶点为 .
.
 的代数式表示)
的代数式表示) 并以
并以 ,当
,当 时,请判断⊙
时,请判断⊙ 是抛物线上任意一点,过
是抛物线上任意一点,过 . 那么是否存在这样的点
. 那么是否存在这样的点 与以
与以
 交
交 轴于
轴于 、
、 两点,交
两点,交 轴于点
轴于点 ,顶点为
,顶点为 .
.
 的代数式表示)
的代数式表示) 并以
并以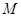 ,当
,当 时,请判断⊙
时,请判断⊙ 是抛物线上任意一点,过
是抛物线上任意一点,过 . 那么是否存在这样的点
. 那么是否存在这样的点 与以
与以 交
交 轴于
轴于 、
、 两点,交
两点,交 轴于点
轴于点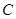 ,已知抛物线的对称轴为
,已知抛物线的对称轴为 ,
, ,
, ,
, ,使点
,使点 两点,若以
两点,若以 为直径的圆恰好与
为直径的圆恰好与
 交
交 轴于
轴于 、
、 两点,交
两点,交 轴于点
轴于点 ,已知抛物线的对称轴为
,已知抛物线的对称轴为 ,
, ,
, ,
, ,使点
,使点 两点,若以
两点,若以 为直径的圆恰好与
为直径的圆恰好与

 交
交 轴于
轴于 、
、 两点,交
两点,交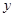 轴于点
轴于点 ,顶点为
,顶点为 .
.
 的代数式表示)
的代数式表示) 并以
并以 ,当
,当 时,请判断⊙
时,请判断⊙ 是抛物线上任意一点,过
是抛物线上任意一点,过 . 那么是否存在这样的点
. 那么是否存在这样的点 与以
与以