题目内容
抛物线 交
交 轴于
轴于 、
、 两点,交
两点,交 轴于点
轴于点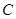 ,已知抛物线的对称轴为
,已知抛物线的对称轴为 ,
, ,
, ,
,
(1)求二次函数 的解析式;
的解析式;
在抛物线对称轴上是否存在一点 ,使点
,使点 到
到 、
、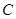 两点距离之差最大?若存在,求出
两点距离之差最大?若存在,求出 点坐标;若不存在,请说明理由;
点坐标;若不存在,请说明理由;
平行于 轴的一条直线交抛物线于
轴的一条直线交抛物线于 两点,若以
两点,若以 为直径的圆恰好与
为直径的圆恰好与 轴相切,求此圆的半径.
轴相切,求此圆的半径.
(1)将 代入
代入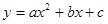 ,
,
得 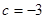 .
.
将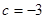 ,
, 代入
代入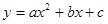 ,
,
得 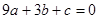 .……….(1)
.……….(1)
∵ 是对称轴,
是对称轴,
∴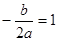 . (2)
. (2)
将(2)代入(1)得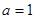 ,
, 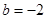 .
.
所以,二次函数得解析式是 .
.
(2)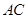 与对称轴的交点
与对称轴的交点 即为到
即为到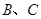 的距离之差最大的点.
的距离之差最大的点.
∵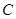 点的坐标为
点的坐标为 ,
, 点的坐标为
点的坐标为 ,
,
∴ 直线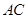 的解析式是
的解析式是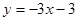 ,
,
又对称轴为 ,
,
∴ 点 的坐标
的坐标 .
.
(3)设 、
、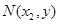 ,所求圆的半径为r,
,所求圆的半径为r,
则 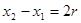 ,……………(1)
,……………(1)
∵ 对称轴为 ,
,
∴ 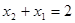 . ……………(2)
. ……………(2)
由(1)、(2)得: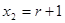 .………(3)
.………(3)
将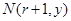 代入解析式
代入解析式 ,
,
得 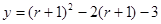 ,…………(4)
,…………(4)
整理得:  .
.
由于 r=±y,当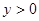 时,
时,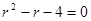 ,
,
解得,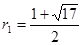 ,
, 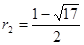 (舍去),
(舍去),
当 时,
时,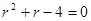 ,
,
解得,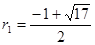 ,
, 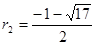 (舍去).
(舍去).
所以圆的半径是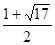 或
或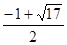 .
.
解析

练习册系列答案
相关题目

 交
交 轴于
轴于 、
、 两点,交
两点,交 轴于点
轴于点 ,顶点为
,顶点为 .
.
 的代数式表示)
的代数式表示) 并以
并以 ,当
,当 时,请判断⊙
时,请判断⊙ 是抛物线上任意一点,过
是抛物线上任意一点,过 . 那么是否存在这样的点
. 那么是否存在这样的点 与以
与以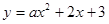
 交
交 轴于
轴于 、
、 两点,交
两点,交 轴于点
轴于点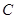 ,顶点为
,顶点为 .
.
 的代数式表示)
的代数式表示) 并以
并以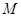 ,当
,当 时,请判断⊙
时,请判断⊙ 是抛物线上任意一点,过
是抛物线上任意一点,过 . 那么是否存在这样的点
. 那么是否存在这样的点 与以
与以 交
交 轴于
轴于 、
、 两点,交
两点,交 轴于点
轴于点 ,已知抛物线的对称轴为
,已知抛物线的对称轴为 ,
, ,
, ,
, ,使点
,使点 两点,若以
两点,若以 为直径的圆恰好与
为直径的圆恰好与

 交
交 轴于
轴于 、
、 两点,交
两点,交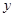 轴于点
轴于点 ,顶点为
,顶点为 .
.
 的代数式表示)
的代数式表示) 并以
并以 ,当
,当 时,请判断⊙
时,请判断⊙ 是抛物线上任意一点,过
是抛物线上任意一点,过 . 那么是否存在这样的点
. 那么是否存在这样的点 与以
与以