题目内容
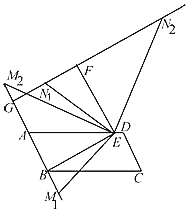
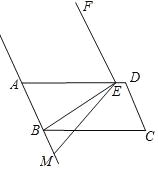
【题目】如图,四边形ABCD为平行四边形,过点B作BE⊥AB交AD于点E,将线段BE绕点E顺时针旋转90°到EF的位置,点M(点M不与点B重合)在直线AB上,连结EM.
(1)当点M在线段AB的延长线上时,将线段EM绕点E顺时针旋转90°到EN1的位置,连结FN1,在图中画出图形,求证:FN1⊥AB;
(2)当点M在线段BA的延长线上时,将线段EM绕点E顺时针旋转90°到EN2的位置,连结FN2,在图中画出图形,点N2在直线FN1上吗?请说明理由;
(3)若AB=3,AD=6,DE=1,设BM=x,在(1)、(2)的条件下,试用含x的代数式表示△FMN的面积.
【答案】(1)证明见解析;(2)点N2在直线FN1上;(3)S1=2x+![]() x2(x>0);S2=2x-
x2(x>0);S2=2x-![]() x2(3<x<4);S3=
x2(3<x<4);S3=![]() x2-2x(x>4).
x2-2x(x>4).
【解析】
(1)首先证明△EBM1≌△EFN1,再证明四边形BEFG为矩形,因此证明FN1⊥AB.
(2)首先证明△EBM2≌△EFN2,即可得∠EFN2=90°,再根据∠EFN1+∠EFN2=180°,即可得点N2在直线FN1上.
(3)根据(1)的四边形BEFG为正方形,即可计算AE,再利用在Rt△ABE中,结合勾股定理计算BE,进而分情况讨论.
(1)证明:如图,∵∠BEF=∠M1EN1=90°,
∴∠BEM1=∠FEN1,
∵DB=DF,EM1=EN1
∴△EBM1≌△EFN1,
∴∠EFN1=∠EBM1,
∵EB⊥AB,
∴∠EBM1=90°
∴∠EFN1=90°,
∴四边形BEFG为矩形,
∴∠FGB=90°
即FN1⊥AB.
(2)如图,跟(1)同理可证△EBM2≌△EFN2,则∠EFN2=90°,
由于∠EFN1+∠EFN2=180°,所以点N2在直线FN1上.
(3)由(1)可知四边形BEFG为正方形,
∵AD=6,DE=1,
∴AE=5,
在Rt△ABE中,BE=![]() =4,
=4,
当点M1在线段AB的延长线上时,S1=![]() x(4+x)=2x+
x(4+x)=2x+![]() x2,此时x>0;
x2,此时x>0;
当点M2在线段BA的延长线上时,
①当3<x<4时,S2=![]() x(4-x)=2x-
x(4-x)=2x-![]() x2.
x2.
②当x>4时,S3=![]() x(x-4)=
x(x-4)=![]() x2-2x.
x2-2x.